Induktion und Induktionsgesetze

Auf den Seiten zum Elektromagnetismus und zu den Magnetfeldgrößen ist beschrieben, dass ein Strom durchflossener Leiter von einem Magnetfeld umgeben ist. Elektrischer Strom und Magnetfelder stehen im Zusammenhang. Praktische Versuche führten zu folgenden Beobachtungen:

1. Wird ein metallischer Leiter so durch ein ruhendes statisches Magnetfeld bewegt, dass er die Feldlinien quer schneidet, dann ist an den Leiterenden eine Spannung messbar. Ist der Leiter Teil eines Stromkreises oder bildet er eine in sich geschlossene Leiterschleife, dann fließt elektrischer Strom. Dieses Verhalten wird als Induktion der 1. Art bezeichnet und mit der Lorentzkraft erklärt. Sie wirkt auf bewegte Ladungen.
2. Ruht der Leiter oder die Leiterschleife und wird das statische Magnetfeld so bewegt, dass die Feldlinien den Leiter quer zur Feldrichtung schneiden, wo entsteht an den Leiterenden eine Spannung und in einer geschlossenen Leiterschleife fließt Strom.
3. In einer weiteren Versuchsvariante sind sowohl der Leiter oder die Leiterschleife als auch das Magnetfeld ortsstabil. Die Feldstärke des Magnetfelds ist die veränderliche Größe. An den Leiterenden ist eine Induktionsspannung messbar und in der geschlossenen Leiterschleife fließt Strom.

In den beiden letzten Beispielen bewegen sich makroskopisch keine Ladungsträger. Es gibt keine Strompfade deren Magnetfelder sich mit dem äußeren Magnetfeld überlagern können. Mit der Lorentzkraft ist die Erklärung nicht möglich. Die Beobachtung wird als Induktion der 2. Art bezeichnet und nachfolgend erklärt.

Faradaysches Induktionsgesetz

Die Beobachtungen gehören zum Naturgesetz der elektromagnetischen Induktion. Der magnetische Fluss Φ ist eine skalare Größe und steht für die Anzahl der Magnetfeldlinien, die vereinfacht angenommen senkrecht durch eine definierte Fläche gehen. In der Skizze soll es die hellgelbe Fläche A sein. In diesem Bereich wird die Stärke des Magnetfelds durch die vektorielle Flussdichte B beschrieben. Der magnetische Fluss Φ ist proportional zur Flussdichte B und zur Fläche A. Für ein homogenes Magnetfeld und einer dazu senkrechten ebenen Fläche ist Φ das Skalarprodukt der Flussdichte B mit dem Flächennormalvektor. Der Normal(en)vektor (rot) steht immer senkrecht auf der seiner Fläche. Die effektiv wirksame Fläche ist das Skalarprodukt zwischen der Fläche, der Feldrichtung und dem Kosinus des Winkels zwischen dem Flächennormalvektor und der Feldrichtung. Die effektiv wirksame Fläche ist maximal wenn die Feldlinien senkrecht durch diese Fläche gehen. Steht die Fläche parallel zur Feldrichtung, dann ist die effektiv wirksame Fläche für cos(90°) null. Der magnetische Fluss Φ für diesen Winkel ist null.

Ändert sich das Magnetfeld, so entsteht in seinem Bereich ein elektrisches Feld. Es ist wie das B-Feld ein Wirbelfeld ohne Quellen und Senken. Die Rotationsrichtung kann mit der Rechten-Hand-Regel bestimmt werden. Der Daumen zeigt in Richtung des sich positiv ändernden Magnetfelds. Angewendet auf die Skizze würden die geschlossenen Finger entgegen dem Uhrzeigersinn weisen. Nach der Lenzschen Regel und dem Energieerhaltungssatz ist der tatsächliche Drehsinn wie eingezeichnet im Uhrzeigersinn.

Wird mit der Linken-Hand-Regel die Wirbelfeldrichtung bestimmt, dann zeigt sich sogleich die Drehrichtung im Uhrzeigersinn. Die beiden Regeln bilden keinen Widerspruch. Wird die Linke-Hand-Regel angewendet, dann sind die Bewegungsrichtung der Elektronen und damit der Elektronenstrom von Minus nach Plus gemeint. Mit der Rechten-Hand-Regel wird die Bewegungsrichtung positiver Ladungen betrachtet in Übereinstimmung mit der Richtung des elektrischen Felds von Plus nach Minus.

In der Skizze ist der Feldverlauf durch die blauen geschlossenen Feldlinien angedeutet. Es gibt keine elektrischen Leiter, keine freien Ladungsträger und keinen Strom. Das elektrische Wirbelfeld ist an keine freien Ladungsträger gebunden. Die Wechselwirkungen zwischen dynamischen magnetischen und induzierten elektrischen Wirbelfeldern ermöglichen die Übertragung elektromagnetischer Funkwellen durch ein Vakuum (z.B. Satellitenfunk, WLAN ...). Für den geschlossenen äußeren Rand der Fläche A im elektrischen Wirbelfeld (blau) errechnet sich die elektrische Feldstärke mathematisch durch Integration aller infinitesimaler Teilfeldstärken und Wegelemente.

Induktion der 2. Art

Ortsfest ändert sich nur die magnetische Flussdichte B und erzeugt ein elektrisches Wirbelfeld. Die zuvor aufgestellte Behauptung für die Rotationsrichtung des elektrischen Wirbelfelds soll mithilfe der folgenden Skizze näher erklärt werden. In das elektrische Wirbelfeld wird eine praktisch offene Leiterschleife gebracht, sodass die E-Feldlinien parallel zur Leiterschleife verlaufen. Der Stromkreis wird durch ein hochohmiges Voltmeter geschlossen. Die Leiterschleife bleibt ortsfest und bildet den Rand einer ebenen Fläche, die vom sich ändernden B-Feld senkrecht durchlaufen wird. Das B-Feld nimmt in Blickrichtung von unten nach oben zu. Die Rotationsrichtung des elektrischen Wirbelfelds (blau) verläuft wie im Bild zuvor im Uhrzeigersinn. Die im Leiterwerkstoff freien Elektronen bewegen sich entgegengesetzt zum Drehsinn des E-Wirbelfelds. Das untere Leiterende erhält dadurch ein negatives und das obere Ende ein positives Ladungspotenzial. Zwischen den offenen Leiterenden entsteht die Induktionsspannung Uind vergleichbar mit einem statischen E-Feld zwischen den Polen.

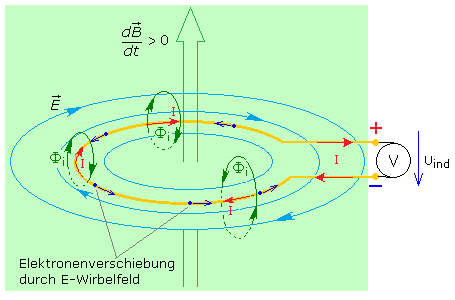
Ist die Änderungsrate des B-Feld konstant, dann stellt sich zwischen dem elektrischen Wirbelfeld und dem statischen E-Feld ein Gleichgewicht ein. Die Induktionsspannung erreicht einen konstanten Wert. Dieser Vorgang wird als Induktion 2. Art bezeichnet. Die offene Leiterschleife wird zur Spannungsquelle mit Uind. Das Spannungsmessgerät schließt den Stromkreis und der Induktionsstrom I (rot) fließt vom Pluspol durch das Messgerät zum Minuspol und weiter durch die Drahtschleife zurück. Dieser Strom generiert um die Leiterschleife ein konzentrisches Magnetfeld (dunkelgrün) in der eingezeichneten Drehrichtung. Sie wird mit der Rechten-Hand-Regel bestimmt. Innerhalb der Leiterschleife ist der vom Strom erzeugte magnetische Fluss Φi dem äußeren Erregerfeld entgegengerichtet. Die Lenzsche Regel und der Energieerhaltungssatz sind erfüllt.

Das elektrische Wirbelfeld bewegt Elektronen entgegen der Rotationsrichtung. Die maximale Induktionsspannung an den Leiterenden entsteht, wenn die offene Leiterschleife parallel im Winkel von 0° zum Wirbelfeld liegt. Wird die Leiterschleife um 90° zum E-Feld gedreht, dann kann es keine Ladungsträger in Richtung zu den Leiterenden trennen. Es entsteht keine Induktionsspannung. In dieser Anordnung steht die Leiterschleife mit den unbewegten Ladungsträgern parallel zum B-Feld. Ruhende Ladungsträger bilden kein Magnetfeld aus, sodass die B-Feldänderung keine Induktionsspannung erzeugen kann.

Induktion durch Leiterbewegung im ruhenden Magnetfeld

Wird ein gerader metallischer Leiter quer durch ein homogenes Magnetfeld bewegt, dann ist an den Leiterenden eine kleine Spannung messbar. Mit dem Leiter bewegen sich die darin freien Elektronen in definierter Richtung und das entspricht einem elektrischen Strom. Jeder elektrische Strom ist senkrecht zur Stromrichtung von einem konzentrischen Magnetfeld umgeben. Das äußere Magnetfeld und das der bewegten Elektronen überlagert sich und die Ladungsträger erfahren eine Kraft. Im metallischen Leiter kann diese Kraft nur die Elektronen verschieben, wobei ein Leiterende einen negativen Ladungsüberschuss erhält. Zwischen beiden Leiterenden entsteht eine Potenzialdifferenz, die Induktionsspannung.

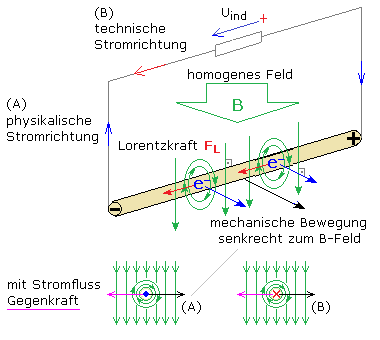
Die Lorentzkraft

Die Lorentzkraft FL wirkt auf bewegte Ladungen q. FL ist proportional zur Stärke des Magnetfelds B und zur Geschwindigkeit v mit der sich die Ladung im homogenen B-Feld rechtwinklig zur Feldrichtung bewegt. Wird ein Leiter(stab) der Länge s mit konstanter Geschwindigkeit quer durch dieses B-Feld gezogen, so kommt es im Leiter zur Ladungstrennung. Das eine Ende erhält einen negativen Ladungsüberschuss und das andere Ende wird entsprechend positiv geladen. Diese Potenzialdifferenz steht mit einem elektrischen Feld E zwischen den offenen Leiterenden in Verbindung. Die elektrische Feldstärke ist definiert als Spannung dividiert durch den Abstand der Ladungen, hier der Leiterlänge s im Magnetfeld. Solange dieser Leiterabschnitt mit konstanter Geschwindigkeit das homogene B-Feld senkrecht schneidet, kommt es zwischen der Lorentzkraft und der E-Feldkraft zum Gleichgewicht. Damit kann eine Gleichung zur Berechnung der Induktionsspannung hergeleitet werden. Die Potenzialdifferenz zwischen den Leiterenden ist die Induktionsspannung Uind.

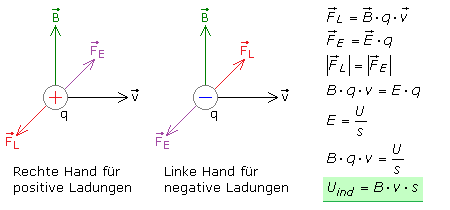
Die Kraftrichtung der Lorentzkraft FL kann mit der Rechten-Hand-Regel für positive Ladungen und entsprechend mit der Linken-Hand-Regel für negative Ladungen ermittelt werden. Ebenso anwendbar ist die Dreifinger UVW-Regel. Der maximale Effekt entsteht, wenn alle Größen zueinander rechtwinklig ausgerichtet sind. Die folgende Skizze zeigt, dass mit beiden Regeln die Richtung der Lorentzkraft auf Ladungen im bewegten Leiter ermittelt werden kann. Zusätzlich ist die Herleitung für die Induktionsspannung angegeben.

Bei der Hand-Regel ist die Ursache das Magnetfeld und tritt in die offene Handfläche ein. Der abgespreizt Daumen zeigt in die mechanische Bewegungsrichtung. Die gestreckten Finger zeigen die Bewegungsrichtung der Ladungsträger an. Für die rechte Hand sind es positive und für die linke Hand negative Ladungen.

Bei der Dreifinger UVW-Regel steht der Daumen für die Ursache und zeigt die mechanische Bewegungsrichtung an. Der senkrecht gestellte Zeigefinger entspricht der Vermittlung und zeigt die Magnetfeldrichtung von Nord nach Süd an. Der zu beiden senkrecht gestellte Mittelfinger steht für die Wirkung und zeigt die Bewegungsrichtung FL der Ladungsträger an. Mit der rechten Hand sind es positive und mit der linken Hand negative Ladungen.

Wird die Bewegungsrichtung des Leiters oder die Magnetfeldrichtung um 180° geändert, dann kehrt sich auch die Polarität für Uind um. Nach der Lenzschen Regel und den wissenschaftlich mathematischen Herleitungen mithilfe der Maxwell-Gleichungen ist Uind negativ definiert. Wird die Induktionsspannung in einem externen Stromkreis genutzt, dann entspricht der mechanisch bewegte Leiter einer Spannungsquelle. Im Laststromkreis fließt elektrischer Strom und erzeugt um den bewegten Leiter herum ein konzentrisches Magnetfeld. Es überlagert sich mit dem homogenen äußeren B-Feld, wobei der Leiterstab eine Bewegungskraft erfährt. Sie ist der Zugkraft entgegen gerichtet, die den Leiter mit v durch das Magnetfeld bewegt. Wäre es nicht so, käme es zu einer Selbstverstärkung und der Energieerhaltungssatz des geschlossenen Systems wäre nicht erfüllt.

In der folgenden Skizze ist der Leiter stark vergrößert, um die Bewegungsrichtung einzelner Elektronen besser zu verdeutlichen. Die Feldrichtung des B-Felds verläuft von vorne nach hinten. Das offene Leiterstück bewegt sich mit konstanter Geschwindigkeit v nach rechts senkrecht zum B-Feld. Das obere waagerechte Leiterstück schneidet das homogene Magnetfeld längs der Feldlinien. Nach der Linken-Hand-Regel für negative Ladungen wirkt die Lorentzkraft FL dann in Richtung der Leiterlängsseite. Die beeinflussten Elektronen werden nicht zu den unteren Leiterenden transportiert und tragen nicht zur Induktionsspannung bei. Im mittleren Bildteil schneiden die beiden parallelen Leiterteile der offenen Leiterschleife das B-Feld quer. Da die Elektronen gleichermaßen zu beiden offenen Leiterenden verschoben werden, entsteht dort keine Potenzialdifferenz. An den Leiterenden kann keine Induktionsspannung gemessen werden.

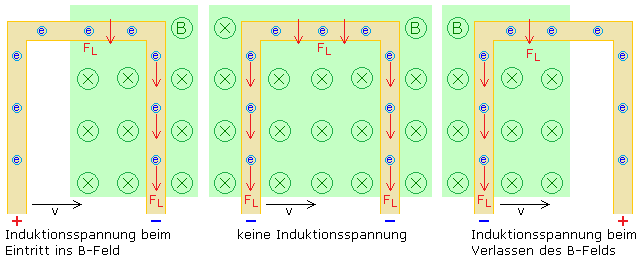
Praktische Versuche zeigen, dass die Induktionsspannung direkt proportional zur Geschwindigkeit ist, mit der ein Leiter das ruhende homogene Magnetfeld quer schneidet. Bei einer Leiterschleife wird nur dann eine Induktionsspannung generiert, solange sich ein wirksamer Teil der Schleife im Magnetfeld bewegt. Die Induktionsspannung hat eine bestimmte Polarität und bleibt konstant, solange die Geschwindigkeit und das homogene Magnetfeld konstant sind. Im linken Bildteil bewegt sich ein wirksamer Teil der Leiterschleife im Magnetfeld. Durch die Lorentzkraft wird das rechte Leiterende negativ gegenüber dem linken Ende außerhalb des B-Felds. Im rechten Bildteil hat dieser Leiterabschnitt das Magnetfeld verlassen und die Ladungsträger im linken Leiterabschnitt erfahren die Lorentzkraft. Dieses Leiterende wird negativer und die Induktionsspannung wechselt die Polarität.

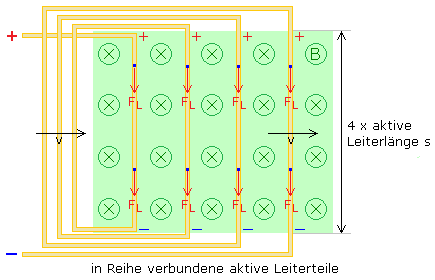
Die Induktionsspannung ist direkt proportional zu der im B-Feld wirksamen Leiterlänge. Die Grafik oben in der Mitte zeigt, dass ein in Schleifen gelegter Leiter länger ist, aber keine Induktionsspannung generiert, wenn sich diese Schleifen komplett im B-Feld bewegen. Die folgende Grafik zeigt eine Spule mit 4 in Reihe geschalteten Leiterschleifen. Bewegt sie sich durch ein homogenes Magnetfeld, so generiert sie eine proportional zur Windungszahl höhere konstante Induktionsspannung solange nur die hier wirksamen 4 Leiterteile der Länge s die B-Feldlinien schneiden.

Mathematische Zusammenhänge

Die Induktionsspannung ist direkt proportional zum magnetischen Fluss Φ, der Anzahl der Feldlinien. Das damit im Zusammenhang stehende B-Feld, die magnetische Flussdichte ist der Fluss Φ, der von einer bestimmten Fläche A umfasst wird. Die Betrachtung vereinfacht sich, wenn die Feldlinien das Flächenelement senkrecht durchlaufen. In die allgemeine Definition für Uind eingesetzt folgt Gl. (1), wo sowohl B als auch A zeitlich veränderlich sein können. Die Ableitung nach der Zeit erfolgt mit der Produktregel und führt zur Gl. (2).

Die Induktionsspannung entsteht nach Gl. (2) durch zeitliche Änderungen des Flusses B(t), der Fluss umfassenden Fläche A(t) oder beider Größen. Im ersten Spezialfall soll das B-Feld homogen und konstant, also zeitlich unabhängig sein. Die Ableitung B(t) im ersten Klammerausdruck der Gl. (2) ist dann null. Es bleibt die zeitliche Änderung der Fläche A(t) im zweiten Klammerausdruck. Dieses Flächenelement soll sich senkrecht zum B-Feld bewegen.

Wird nur ein Leiterstück oder wie weiter oben skizziert der aktive Teil eines Spulenrahmens mit konstanter Geschwindigkeit v = s/t durch das B-Feld bewegt, dann wirkt nur dort die Lorentzkraft und generiert die Induktionsspannung. Nicht die Fläche des Leiters ändert sich sondern die Wegstrecke Δs, die das Leiterelement im B-Feld zurücklegt. Die im B-Feld wirksame Leiterlänge l multipliziert mit der Wegstrecke Δs kann als sich änderndes Flächenelement angesehen werden. Die mathematische Herleitung ergibt die weiter oben und in Formelsammlungen zu findende Gleichung zur Berechnung der Induktionsspannung.

Im zweiten Spezialfall soll die offene Leiterschleife oder Spule ruhen. Sie wird von einem sich gleichförmig ändernden Magnetfluss durchsetzt. Die Leiter bilden den Außenrand einer Fläche, die senkrecht von den Feldlinien durchsetzt wird. Im Klammerausdruck der Gl. (2) ist dann der zweite Summand null. Solange sich der Magnetfluss Φ linear zunehmend ändert, wird an den Leiteranschlüssen eine negative Induktionsspannung generiert. Nimmt der Magnetfluss linear ab, dann ändert die Induktionsspannung ihre Polarität.

Der Videoclip zeigt dies Induktionsvorgänge bei einer Leiterschleife und Luftspule für den sich linear ändernden Magnetfluss. Der in der Leiterschleife geschlossene blaue Kreis ist das elektrische Wirbelfeld, das von der Flussänderung erzeugt wird. Die freien Leiterelektronen erfahren die dazu entgegen gerichtete Lorentzkraft und an den offenen Anschlüssen ist die Induktionsspannung messbar. Die individuelle Steuerung kann mithilfe der einblendbaren Controlleiste erfolgen.

Das Induktionsgesetz gilt auch für eine sich im Magnetfeld drehende Leiterschleife oder Spulenwicklung. Weitere Informationen dazu können im Kapitel zum Prinzip elektrischer Generatoren nachgelesen werden.

Wirbelströme

Die elektromagnetische Induktion entsteht in allen metallischen Leitern, die einer magnetischen Flussänderung ausgesetzt sind. Schwingt eine Metallscheibe durch die Polschuhe eines Magneten, so wird in der Scheibe eine Spannung induziert. Die Induktionsspannung wechselt die Polarität beim Eintreten und Verlassen des Magnetfelds. Der ohmsche Widerstandswert einer Metallscheibe ist sehr gering, sodass in ihr hohe Induktionsströme auftreten. Da es in der Metallscheibe keine festgelegten Stromwege gibt, wird der Strom als Wirbelstrom bezeichnet.

Wirbelströme werden technisch bei der Wirbelstrombremse ausgenutzt. Das kann eine auf der Motorachse befestigte Kupferscheibe sein, die sich nach Abschalten der Antriebskraft in einem zugeschalteten Magnetfeld dreht. Der Induktionsstrom in der Scheibe bremst den Motor berührungslos und erzeugt proportional Wärmeenergie.

Die sogenannten analogen Stromzähler im Haushalt nutzen ebenfalls das Wirbelstromprinzip. Eine Aluminiumscheibe dreht sich vom jeweiligen Strombedarf angetrieben im Feld eines Dauermagneten von dem es kalibriert gebremst wird. Die Aluscheibe ist mit dem Zählwerk verbunden. Diese Leistungszähler werden gesetzlich bis zum Jahr 2032 durch Digitalzähler ersetzt.

Bei vielen inzwischen alten Zeigermessinstrumenten wird das Schwingen der empfindlichen Messwerke durch Wirbelströme gedämpft. Zwischen den Polen des Dauermagneten dreht sich ein geschlossener Aluminiumrahmen, der gleichzeitig auch Wickelkörper der Messwerkspule ist.

In einem magnetischen Wechselfeld können Metallwerkstücke durch Wirbelströme so erhitzt werden, dass man diesen Vorgang zur thermischen Induktionshärtung nutzt. Rohsiliziumstäbe (Halbleiter) werden durch die Induktionsschmelze zu hochreinem Silizium veredelt. Die Stäbe durchwandern langsam ein Hochfrequenzmagnetfeld. Sie werden dabei aufgeschmolzen und die Verunreinigungen reichern sich im kälteren Stabende an.

Nicht immer ist dieser Wärmeeffekt erwünscht. Bei Transformatoren und Motoren sind Wirbelströme unerwünscht und verringern die Nutzleistung. Zur Verhinderung werden die Trafokerne und Motorenanker aus vielen gegeneinander isolierten Formblechen zusammengesetzt. Verglichen mit einem massiven Kern hat die lamellierte Bauart einen höheren ohmschen Widerstandswert. Die Wirbelströme verringern sich, die magnetische Leitfähigkeit bleibt hoch. Das Kernmaterial für Hochfrequenzübertrager und Spulen besteht aus Ferrit. Dieses sehr gut magnetisierbare Material verhält sich eher wie ein Isolator, da alle kleinen Metallteilchen von nicht leitender Keramik umschlossen sind.