Einfache Konstantspannungsquelle mit Z-Diode
Fast alle elektronischen Schaltungen sind auf konstante Betriebsspannungen angewiesen. Oft sollen es optimale Gleichspannungen sein. Batterien und Akkumulatoren sind chemische Elemente und stellen nur für eine begrenzte Zeit konstante absolute Gleichspannungen bereit. Sie sind nicht alterungsbeständig und mit dem Grad ihrer Entladung nimmt ihr Innenwiderstand zu und die Klemmenspannung ab. Dieser immer vorhandene Innenwiderstand bestimmt die Spannungskonstanz bei wechselnder Belastung. Wird die Versorgungsspannung von einem einfachen Netzteil erzeugt, so kommen neben primärseitigen Schwankungen der Netzspannung auch geringe und störende Wechselspannungsanteile bis an den Ausgang.
Jede reale Spannungsquelle kann als ideale Konstantspannungsquelle mit einem in Reihe liegenden Innenwiderstand dargestellt werden. Dieser ist nicht als Bauteil vorhanden, sondern eine individuelle Eigenschaft der Spannungsquelle und im Fall chemischer Elemente nicht konstant. Die immer konstante Urspannung Uo ist im Leerlauf ohne Stromfluss an den Anschlussklemmen messbar. Bei geschlossenem Stromkreis fließt der Strom durch den Lastwiderstand in die Spannungsquelle zurück und dort durch den in Reihe liegenden Innenwiderstand Ri. Nach dem Ohm'schen Gesetz erzeugt der Strom dort die Spannung URi.
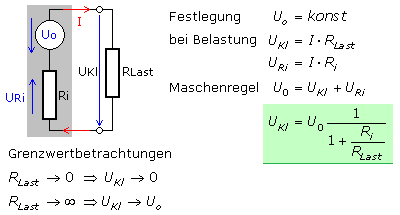
Für die unbelastete Spannungsquelle im Leerlauf gilt immer: \({U_o} = konst\). Früher wurde diese Spannung als Elektromotorische Kraft (EMK) bezeichnet. Im einfachsten Fall stellt der geschlossene Stromkreis eine Reihenschaltung dar, wo nur ein bestimmter Strom fließen kann. Die Stromrichtung im äußeren Stromkreis ist wie eingezeichnet festgelegt und in die gleiche Richtung weisen auch die Spannungszählpfeile an den Widerständen. Der Spannungszählpfeil Uo gehört zum Erzeuger und weist immer in die Gegenrichtung zur Verbraucher Zählpfeilrichtung. Für den Maschenumlauf kann in Richtung des Strompfeils die Spannungssumme aufgestellt werden: \[{U_o} = {U_{Last}} + {U_{Ri}} = I \cdot {R_{Last}} + I \cdot {R_i}\quad \Rightarrow \quad I = \frac{{{U_o}}}{{{R_{Last}} + {R_i}}}\] Die Spannung am Lastwiderstand ist gleich der Klemmenspannung, die bestimmt werden soll: \[{U_o} = {U_{Kl}} + I \cdot {R_i}\quad \Rightarrow \quad {U_{Kl}} = {U_o} - I \cdot {R_i}\] Der Strom I wird ersetzt und zum gewünschten Ergebnis umgeformt: \[{U_{Kl}} = {U_o} - \frac{{{U_o} \cdot {R_i}}}{{{R_{Last}} + {R_i}}} = {U_o}\left( {1 - \frac{{{R_i}}}{{{R_{Last}} + {R_i}}}} \right)\] \[{U_{Kl}} = {U_o}\left( {\frac{{{R_{Last}}}}{{{R_{Last}} + {R_i}}}} \right)\]
Das Ergebnis zeigt, dass nur bei sehr kleinem Innenwiderstand Ri die Klemmenspannung UKl von der Belastung durch RLast weitgehend unabhängig ist. Bei fehlender Last liegt an den Klemmen die konstante Leerlaufspannung Uo an. Bei einem Kurzschluss an den Klemmen hat der Lastwiderstand den Wert null und der Strom erreicht seinen Maximalwert. Er wird vom Innenwiderstand der Quelle begrenzt, sodass URi = Uo wird. An den Anschlussklemmen kann dann keine Spannung gemessen werden.
Eine Konstantspannungsquelle zeichnet sich durch einen sehr kleinen Innenwiderstand aus.
Ihre Urspannung Uo ist zeitlich konstant und unabhängig von der Belastung.
Messtechnische Ermittlung des Innenwiderstands
Wird die oben hergeleitete Gleichung für die Klemmenspannung einer realen Spannungsquelle nach dem Innerwiderstand umgestellt, so ergibt sich eine Bestimmungsgleichung für Ri nach der ΔU/ΔI-Methode: \[{R_i} = \frac{{{U_{Kl}}}}{I} \cdot \left( {\frac{{{U_o}}}{{{U_{Kl}}}} - 1} \right) = \frac{{{U_o}}}{I} - \frac{{{U_{Kl}}}}{I}\quad \Rightarrow \quad {R_i} = \frac{{\Delta {U_{Kl}}}}{{\Delta I}}\] Diese Methode kann immer angewendet werden. Es wird die Klemmenspannung im Leerlauf gemessen, danach werden die kleinere Klemmenspannung und der Strom bei Belastung gemessen. Es können ebenso für zwei unterschiedliche Belastungen die Klemmenspannungen und die zugehörigen Ströme gemessen werden. Aus dem Verhältnis berechnet sich dann der Innenwiderstand der Quelle.
Bei Spannungsquellen mit nicht zu kleinem Innenwiderstand kann nach der Methode der halben Klemmenspannung und dem Messen des Lastwiderstandes mittels Ohmmeter der Innenwiderstand direkt bestimmt werden. Die Quelle wird mit einem variablen Widerstand solange belastet, bis die Klemmenspannung nur noch den halben Wert der Leerlaufspannung anzeigt. \[{U_o} = ({R_i} + {R_{Last}}) \cdot I\] Der Wert des Lastwiderstands ist dann gleich dem Innenwiderstand der Quelle: Wenn RLast = Ri ist, dann gilt: \[{U_o} = 2 \cdot {R_{Last}} \cdot I\quad \Rightarrow \quad {R_{Last}} \cdot I = {U_{Kl}} = \frac{{{U_o}}}{2}\] An anderer Stelle dieses Webprojekts wird mit einem Videoclip der Zusammenhang zwischen Lastwiderstand und Innenwiderstand einer Gleichspannungsquelle schrittweise dargestellt.
Konstantspannung mithilfe einer Z-Diode
Mit einer Zenerdiode kann die Ausgangsgleichspannung in einem weiten Bereich konstant gehalten werden. Dazu sind folgende Bedingungen zu erfüllen:
Die Eingangsspannung muss immer größer als die Z-Spannung der Diode sein.
Der Arbeitsbereich der Z-Diode muss im linearen Bereich der Sperrkennlinie liegen.
Die maximale Verlustleistung der Z-Diode darf nicht überschritten werden.
Ein funktionell minimaler Diodenstrom darf nicht unterschritten werden.
Die Kennlinie einer Z-Diode zeigt im Sperrbereich einen charakteristischen Spannungsdurchbruch mit sehr steilem Stromanstieg. Dieser Kennlinienbereich zeichnet sich durch einen kleinen differenziellen Widerstand aus: \({r_z} = \Delta {U_z}/\Delta {I_z}\). Die Stabilitätsdiode wird mit einem Vorwiderstand an die Eingangsspannung angeschlossen. Er begrenzt den Diodenstrom bei der höchsten zu erwartenden Eingangsspannung auf den maximal erlaubten Sperrstrom. Er oder die maximale Verlustleistung ist im Datenblatt der Diode angegeben. Da der Lastwiderstand parallel zur Z-Diode geschaltet ist, wird die Schaltung als Parallel-Spannungsstabilisierung bezeichnet. Die Z-Diode kann wegen ihres kleinen differenziellen Widerstands ihre Z-Spannung innerhalb größerer Ausgangsbelastungen konstant halten.
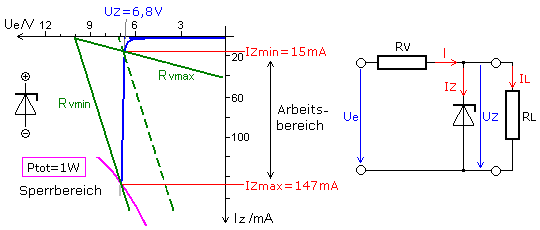
Der Vorwiderstand kann für die unbelastete Schaltung und der erwarteten maximalen Eingangsspannung berechnet werden. Im Datenblatt der Z-Diode ist die maximale Verlustleistung oder der höchste Diodenstrom angegeben. Er fließt im Leerlauf durch die Diode und erzeugt für die dimensionierte Schaltung die maximale Verlustleistung an der Diode: \[{I_{z\,\max }} = \frac{{{U_e} - {U_z}}}{{{R_v}}}\quad \quad {P_{z\,\max }} = {U_z} \cdot {I_{z\,\max }} = {U_z} \cdot \frac{{{U_e} - {U_z}}}{{{R_v}}}\] Für die im Bild dargestellte Schaltung beträgt die maximale Eingangsspannung 10 V. Für die unbelastete Schaltung hat beim maximalen Diodenstrom der Vorwiderstand den Wert Rv min = 22 Ω. Bei belasteter Schaltung teilt sich der Zenerstrom auf. Er wird um den Wert des Laststroms kleiner. Für eine konstante Z-Spannung am Ausgang darf ein minimaler Diodenstrom nicht unterschritten und der lineare Kennlinienbereich nicht verlassen werden. Für die Beispielschaltung beträgt Izmin 10% des maximalen Leerlaufstroms. Bei kurzgeschlossenem Ausgang fließt kein Zenerstrom und die maximale Leistung PRv =4,5 W wird am Vorwiderstand umgesetzt. Die Verlustleistung des Vorwiderstands sollte aus Sicherheitsgründen auf diesen Wert berechnet sein: \[{R_{v\,\min }} = \frac{{{U_e} - {U_Z}}}{{{I_{Z\,\max }}}}\quad \quad {P_{Rv}} = \frac{{U_e^2}}{{{R_v}}}\]
Wird im Kennliniendiagramm die RVmin-Gerade nach rechts nahe zum Beginn des linearen Arbeitsbereichs der Z-Diode verschoben, dann kann an der gestrichelten grünen Widerstandsgeraden die minimale Eingangsspannung von 7,2 V abgelesen werden bei der die Ausgangsspannung noch auf die Z-Diodenspannung stabilisiert ist. Für den Laststrom IL bleiben nur um 3 mA übrig.
Soll die Beispielschaltung bei maximaler Eingangsspannung Ue = 10 V stromsparend betrieben werden, so muss ein größerer Vorwiderstand berechnet werden. Für die eingezeichnete Widerstandsgerade Rvmax darf die Eingangsspannung nicht kleiner werden, da dann der lineare Kennlinienbereich der Z-Diode verlassen wird. Für den Vorwiderstand ist ein Kompromiss zu finden, der eine instabile Eingangsspannung und eine wechselnde Ausgangslast abdeckt. Die zu beachtenden Parameter sind die Z-Spannung, der maximale Zenerstrom und die maximale Eingangsspannung. Für die beiden Extremwerte gilt: \[{R_{v\,\min }} = \frac{{{U_{e\,\max }} - {U_Z}}}{{{I_{Z\,\max }}}}\quad \quad {R_{v\,\max }} = \frac{{{U_{e\,\min }} - {U_Z}}}{{{I_{Z\,\min }} + {I_{L\,\max }}}}\] Eine optimale Stabilisierung wird mit den folgenden Richtlinien zur Dimensionierung erreicht:
Die Eingangsspannung ist mindestens doppelt so groß wie die Z-Spannung.
Bei mittlerer Belastung liegt der Arbeitspunkt in der Mitte der linearen Kennlinie.
Der minimale Zenerstrom darf in keinem Betriebsfall unterschritten werden.
Der Vorwiderstand muss bei der höchsten Eingangsspannung den Diodenstrom auf den maximal erlaubten Zenerstrom begrenzen.
Der Stabilisierungsfaktor
Bei Belastungsänderungen und unstabiler Versorgungsspannung weist die Ausgangsspannung geringe Schwankungen auf. Sie sind umso kleiner, je steiler der Kennlinienverlauf der Z-Diode und je kleiner ihr differenzieller Widerstand im Arbeitsbereich. Er entspricht dem Innenwiderstand einer Spannungsquelle: \[{r_z} = \frac{{\Delta {U_Z}}}{{\Delta {I_Z}}} \approx \frac{{\Delta {U_a}}}{{\Delta {I_L}}} = {r_i}\] Die Qualität der Stabilisierung wird durch einen absoluten Stabilisierungs- oder Glättungsfaktor G beschrieben. Er ist das bei Nennlast messbare Verhältnis der Änderungen der Eingangs- zur Ausgangsspannung und sollte einen hohen Wert haben: \[G = \frac{{\Delta {U_e}}}{{\Delta {U_a}}}\] Sind alle Widerstandswerte bekannt, so kann der Glättungsfaktor berechnet werden. Für die Stabilisierung mit der Z-Diode ist die Ausgangsspannung gleich der Zenerspannung. Wichtig ist der differenzielle Widerstand der Z-Diode im Arbeitsbereich. Er kann aus der Diodenkennlinie ermittelt werden, die im Arbeitsbereich weitgehend linear verläuft. Teilweise wird der Wert auch in den Datenblättern angegeben. \[\begin{array}{l} \Delta {U_e} = \Delta {I_Z} \cdot {R_v} + \Delta {U_Z}\\ \frac{{\Delta {U_e}}}{{\Delta {U_Z}}} = \frac{{\Delta {I_Z}}}{{\Delta {U_Z}}}\,{R_v} + 1\quad \quad {r_z} = \frac{{\Delta {U_Z}}}{{\Delta {I_Z}}}\quad \Rightarrow \end{array}\] \[G = \frac{{\Delta {U_e}}}{{\Delta {U_Z}}} = 1 + \frac{{{R_v}}}{{{r_z}}}\]
Z-Dioden sind von der Temperatur abhängig. Im Normalbetrieb ist der Einfluss oft vernachlässigbar klein. Z-Dioden bis 8 Volt haben negative und oberhalb 8 Volt positive Temperaturkoeffizienten. Die 6,2 Volt Z-Diode ist als einzige praktisch von der Temperatur unabhängig. Die kombinierte Reihenschaltung mehrerer Z-Dioden zur gewünschten Z-Spannung kann den Temperatureinfluss minimieren. Bei hohen Zenerspannungen kann der positive Temperaturkoeffizient der Z-Diode durch eine in Reihe geschaltete normale Si-Diode ausgeglichen werden. Sie hat einen negativen Temperaturbeiwert und ist in Durchlassrichtung zu schalten.
Ist die Ausgangsleistung der einfachen Schaltung zu klein oder die Spannungskonstanz bei größerem Lastwechsel oder weniger stabilen Eingangsspannungen nicht präzise genug, bieten Konstantspannungsquellen mit aktiven Regelverstärkern die Lösung.