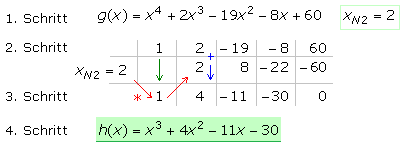
Polynomdivision

In grafischen Darstellungen mathematischer Funktionen, meistens im rechtwinkligen Achsenkreuz, gibt es charakteristische Punkte. Der Schnitt- oder Berührpunkt mit der x-Achse wird allgemein als Nullstelle bezeichnet, wobei der Berührpunkt eine doppelte Nullstelle ist. Für Übertragungsfunktionen der Elektrotechnik, wo mathematische Beziehungen das Verhalten von Ein- und Ausgangssignalen dynamischer Systeme beschreiben, ist neben Nullstellen auch von Polen die Rede. Wie zeigen sie sich in der grafischen Funktionsdarstellung und wie lassen sich Nullstellen und Pole bestimmen, ohne die Funktion per Wertetabelle gleich zeichnen zu müssen? Die Bestimmung der Nullstellen kann mit der Polynomdivision erfolgen.

Nullstellen

Eine mathematische Funktion f(x) hat dort eine Nullstelle, wenn der Wert der Variablen x in die Funktion eingesetzt den Funktionswert null ergibt. Beschränken wir uns zuerst auf einfachere Funktionen, wo die Funktionsvariable x nicht im Nenner vorkommt. Wie viele Nullstellen eine gegebene Funktion hat, ist von der Funktion abhängig.

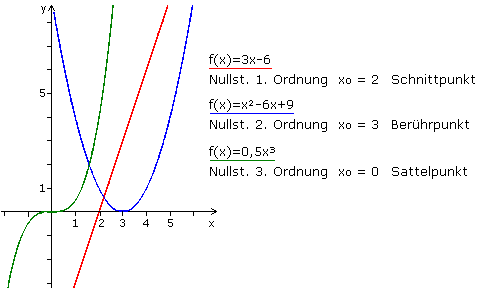
Eine Gerade oder Polynomfunktion 1. Ordnung hat eine einfache Nullstelle mit dem Vielfachen von 1, auch als Nullstelle 1. Ordnung bezeichnet. Zum Beispiel hat die Funktion f(x) = 3·x − 6 ihre einzige Nullstelle bei xo = 2. Die grafische Darstellung schneidet in diesem Punkt die x-Achse und die Funktionswerte wechseln das Vorzeichen.

Die Polynomfunktion 2. Ordnung oder quadratische Funktion f(x) = x² − 6x + 9 = (x−3)² kann zur Bestimmung der Nullstellen in ihre Faktoren verlegt werden: f(x) = (x−3)(x−3). Jeder Faktor ergibt mit xo = 3 eine Nullstelle. Es handelt sich um eine zweifache Nullstelle, eine Nullstelle 2. Ordnung oder dem Vielfachen von 2. In der grafischen Darstellung berührt die Kurve an dieser Stelle die x-Achse und für die Funktionswerte gibt es keinen Vorzeichenwechsel.

Die einfache Polynomfunktion 3. Ordnung f(x) = x³ hat an der Stelle xo = 0 eine dreifache Nullstelle, eine Nullstelle 3. Ordnung oder dem Vielfachen von 3. Der Funktionsgraph schneidet die x-Achse und für die Funktionswerte ergibt sich ein Vorzeichenwechsel.

Mithilfe der mathematischen Kurvendiskussion werden die charakteristischen Punkte eines Funktionsgraphen exakt bestimmt. Zu ihnen gehören auch die Nullstellen. Die Stammfunktion hat eine mehrfache Nullstelle, wenn mindestens eine Ableitfunktion an der gleichen Stelle eine Nullstelle hat. Auf das letzte Beispiel bezogen hat f(x) = x³ die Ableitfunktionen f'(x) = 3x², f''(x) = 6x und f'''(x) = 6. Da die Stammfunktion und ihre ersten beiden Ableitungen an der Stelle xo = 0 Nullstellen haben, handelt es sich für die Stammfunktion um eine Nullstelle 3. Ordnung, dem Vielfachen von3.

Bei Nullstellen mit ungeraden Vielfachen schneidet der Funktionsgraph die x-Achse und die Funktionswerte wechseln das Vorzeichen.
Bei Nullstellen mit geraden Vielfachen berührt der Funktionsgraph die x-Achse und die Funktionswerte wechseln das Vorzeichen nicht.

Definitionslücke

Bei gebrochen rationalen Funktionen steht die Variable x im Ausdruck des Zählers und Nenners. Wird der Wert des Nenners null, dann ist der Funktionswert nicht mehr definiert, denn er strebt gegen unendlich. Die Funktion hat an dieser Stelle eine Definitionslücke, für die es zwei Möglichkeiten gibt. Die Funktion hat eine hebbare Definitionslücke oder es handelt sich um eine Polstelle und der Graph nähert sich einer senkrechten Asymptoten an, die durch diese x-Koordinate verläuft.

Hebbare Definitionslücke

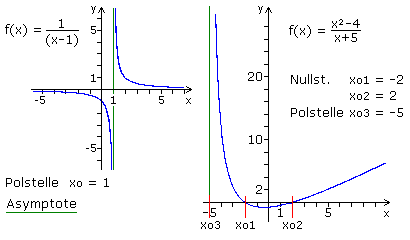
Gibt es im Ausdruck des Zählers und Nenners einer gebrochen rationalen Funktion eine gemeinsame Nullstelle, werden beide Ausdrücke in Linearfaktoren zerlegt und anschließend gekürzt. Bleiben einzelne Nullstellen nur im Nenner bestehen, dann handelt es sich um Polstellen. Dazu das einfache Beispiel einer gebrochen rationalen Funktion f(x) = (x−1) / (x−1)². Für den Zähler und Nenner gibt es mit xo = 1 gleiche Nullstellen. Ob es sich um eine hebbare Definitionslücke handelt, prüft man durch Faktorisieren des Nenners. Man erhält f(x) = (x−1) / (x−1)(x−1) und kann kürzen. Es bleibt die Funktion f(x) = 1 / (x−1) mit einer Nullstelle bei xo = 1 im Nenner, die somit Polstelle ist.

Polstellen

Liegt eine gebrochen rationale Funktion in faktorisierter Form vor, dann ist die Polstelle eine Nullstelle im Ausdruck des Nenners, die nicht gleichzeitig Nullstelle im Zähler ist. Zum Beispiel wird in der gebrochen rationalen Funktion f(x) = (x²−4) / (x+5) der Wert des Zählers für x1 = 2 und x2 = −2 null und somit der Funktionswert zu null. Die Funktion mit Linearfaktoren (faktorisiert) geschrieben kann nicht gekürzt werden. f(x) = (x+2)(x−2) / (x+5). Der Nenner hat für x3 = −5 den Wert null. Die Funktion hat dort eine Definitionslücke, die als Polstelle, Pol oder Unendlichkeitsstelle bezeichnet wird. Der Funktionsgraph nähert sich einer senkrechten Asymptote an, die durch diese Stelle parallel zur y-Achse verläuft.

Wie bei den Nullstellen ordnet man auch den Polstellen eine Ordnungszahl oder Vielfache zu. Die einfache Hyperbelfunktion hat bei xo = 0 eine Nullstelle, die einer Polstelle 1. Ordnung entspricht. Die Funktion f(x) = 1 / (x+1)² hat bei xo = −1 eine doppelte Nullstelle als Polstelle 2. Ordnung.

Bei Polstellen ungerader Ordnung wechseln Funktionswerte beim Überschreiten der Polstelle das Vorzeichen.
Bei Polstellen gerader Ordnung wechseln die Funktionswerte beim Überschreiten der Polstelle das Vorzeichen nicht.

Asymptoten

Nähert sich der Graph einer Funktion weit entfernt vom Koordinatenursprung immer mehr einer anderen Funktion, so wird diese als Asymptote bezeichnet. Der Funktionsgraph kann zwischenzeitlich auch um die Asymptote schwingen und am Ende mit ihr gemeinsam verlaufen. Man untersucht das Verhalten der Funktion im Unendlichen und kann zwischen vier Arten der Asymptoten unterscheiden. Für gebrochen rationale Funktionen vergleicht man dazu die Potenzen des Zählers und Nenners und spricht vom Zähler- und Nennergrad.

Waagerechte Asymptote

Der Zählergrad ist kleiner als der Nennergrad. Die Asymptote verläuft parallel zur x-Achse mit dem Schnittpunkt y = 0.
Der Zählergrad ist gleich dem Nennergrad. Die Asymptote verläuft ebenfalls parallel zur x-Achse. Dividiert man den Koeffizienten der höchsten Potenz des Zählers durch den Koeffizienten der höchsten Potenz des Nenners, so erhält man den Schnittpunkt der Asymptote mit der y-Achse.

Senkrechte Asymptote

Sie zeigt die Unendlichkeitsstelle der Funktion und verläuft als Gerade parallel zur y-Achse durch eine Polstelle. Man erhält sie als Nullstelle des Nenners nach dem Zerlegen der gebrochen rationalen Funktion in Linearfaktoren und dem möglichen Kürzen des Bruchs.

Schiefe Asymptote

Der Zählergrad ist gleich dem Nennergrad + 1. Die schiefe Asymptote wird durch eine allgemeine Geradengleichung beschrieben, an die sich der Funktionsgraph im Unendlichen nähert. Die Geradengleichung erhält man mithilfe der Polynomdivision und einer Grenzwertbetrachtung.

Asymptotische Kurve

Der Zählergrad ist größer als der Nennergrad + 1. An eine kurvenförmige Asymptote nähert sich die gebrochen rationale Funktion weit entfernt vom Koordinatenursprung an. Die Gleichung der Asymptote wird mithilfe der Polynomdivision und einer Grenzwertbetrachtung ermittelt.

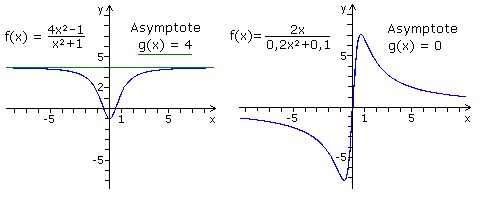
Die Grafik zeigt zwei Beispiele für waagerechte Asymptoten. Links sind Zähler- und Nennergrad gleich und die Asymptote verläuft durch y = 4. Für den Zähler lassen sich zwei Nullstellen bei x1 = -0,5 und x2 = 0,5 bestimmen. Für den Nenner gibt es im Reellen keine Nullstellen. Rechts ist der Zählergrad kleiner als der Nennergrad und die waagerechte Asymptote verläuft bei y = 0 und ist gleich der x-Achse. Aus dem Zähler ergibt sich die Nullstelle im Koordinatenursprung während der Nenner keine reellen Nullstellen hat.

Im Abschnitt zu den Polstellen sind zwei Beispiele zur senkrechten Asymptote. Die Hyperbelfunktion hat eine Polstelle, durch die eine senkrechte Asymptote gezeichnet werden kann, an die sich der Kurvenverlauf immer weiter annähert. Sie hat auch eine waagerechte Asymptote, da ihr Zählergrad kleiner als der Nennergrad ist. Im rechten Funktionsgraphen gibt es an der Polstelle xo3 = −5 eine senkrechte Asymptote.

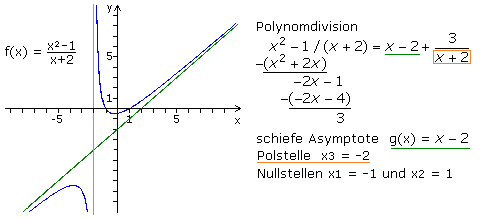
Da für die dargestellte Funktion der Zählergrad gleich dem Nennergrad + 1 ist, gibt es eine schiefe Asymptote. Um ihren Verlauf zu ermitteln, wird der Zähler durch den Nenner dividiert. Bei der Division bleibt ein Restausdruck, der für sehr große x-Werte gegen null strebt. Das Divisionsergebnis ohne diesen Rest ist die Funktionsgleichung der schief liegenden Asymptote. Für den Restausdruck kann im Nenner eine Nullstelle bestimmt werden, die nicht Nullstelle der Funktion ist. Es handelt sich um eine Polstelle bei x3 = −2, durch die eine senkrechte Asymptote verläuft.

Das folgende Bild zeigt den Graphen einer gebrochen rationalen Funktion mit einem Zählergrad größer als der Nennergrad + 1. Die Kurvenäste nähern sich einer parabolischen Asymptote an. Ihre Funktionsgleichung wird mithilfe der Polynomdivision ermittelt, bei der ein Rest bleibt. Für sehr große x-Werte strebt dieser Ausdruck gegen null. Der Nenner hat in dieser Funktion eine Nullstelle, die nicht identisch mit der Nullstelle des Zählers ist. Es handelt sich um einen Pol bei x2 = 0,5 oder Unendlichkeitsstelle, durch die noch eine vertikale Asymptote verläuft.

Mathematische Erklärungen — zu kompliziert?

Sie benötigen mathematische Erkenntnisse und haben mein Webprojekt aufgerufen. Manchmal stellt man fest, dass die Fachmathematik noch nicht richtig sitzt und eine grundsätzlichere Auffrischung gut wäre. Wer also Polynomdivision, Nullstellen berechnen und andere Mathematikthemen online noch einmal nacharbeiten möchte, dem seien die Erklärungen und Mathematik-Übungen auf der Website gut-erklaert.de empfohlen.

Partial- / Polynomdivision

Der binomische Lehrsatz in der Form (a + b)² = a² + 2ab + b² ist sicherlich bekannt. Im Ergebnis stehen drei eingliedrige Ausdrücke mit a und b. Die rechte Seite der Gleichung ist ein Polynom, ein zusammengesetzter mehrgliedriger Ausdruck. Dieses Kapitel befasst sich mit der Division mehrgliedriger Ausdrücke. Soll ein polynomer Zähler durch einen polynomen Nenner dividiert werden, so bringt die partielle Division der einzelnen Zählerausdrücke durch den Nenner kein vereinfachtes Ergebnis. Die Polynomdivision ist nicht Mittel zum Zweck, mit ihr lassen sich Nullstellen für Funktionsgleichungen (Polynome) höherer Ordnung finden. Bei der Grenzwertbetrachtung führt die Polynomdivision zur Funktionsgleichung einer Tangente in einem Kurvenpunkt und damit zur Ableitfunktion.

Ein eindeutig überprüfbares Beispiel ist die Division des binomischen Ausdrucks (a + b)² / (a + b) = a + b.
Kennt man nur das ausmultiplizierte Ergebnis des binomischen Lehrsatzes und soll die Division mit (a + b) durchführen, so ist die Vorgehensweise ähnlich wie bei der schriftlichen Division mehrstelliger Zahlen. Vor der eigentlichen Division ordnet man die Glieder im Zähler und Nenner nach demselben Kriterium. Die allgemeinen Zahlen werden alphabetisch nach fallenden oder steigenden Potenzen sortiert.

Das erste Glied im Ausdruck des Zählers wird durch das erste Glied im Ausdruck des Nenners dividiert. Ziel ist es, das bei der anschließenden Multiplikation des Teilergebnisses mit dem gesamten Nenner ein Ausdruck entsteht, der vom Zähler subtrahiert, sein erstes Glied aufhebt. Mit dem neu entstandenen Zähler verfährt man ebenso. Eine Polynomdivision kann mit dem Rest = 0 aufgehen oder es bleibt ein Rest bestehen. Das Verfahren wird am oben genannten Beispiel schrittweise durchgeführt. Die Glieder liegen schon geordnet vor.

Die Division von a² des linken Ausdrucks durch a ergibt das Teilergebnis a. Es wird mit dem Nenner (a + b) multipliziert und das Ergebnis vom Zähler subtrahiert, wobei man (ab) erhält. Der Rest des Zählers wird angehängt, dabei entsteht (ab + b²). Es wird wieder durch a dividiert mit dem Teilergebnis b. Nach der Multiplikation mit dem Nenner wird subtrahiert, wobei die Rechnung restlos aufgeht. Man erhält das von oben her erwartete Ergebnis (a + b).

Nullstellenbestimmung bei Polynomfunktionen höherer Ordnung

Die Nullstelle einer linearen Funktion zu bestimmen ist einfach. Die Funktionsgleichung y = f(x) wird null gesetzt und der Wert für x an der Stelle Null ausgerechnet. Mit etwas mehr Rechenaufwand unter Anwendung der p-q–Formel können bei einer quadratischen Funktion, der Parabel, vorhandene Nullstellen ermittelt werden. Enthält die Funktionsgleichung höhere Potenzen, kann die Polynomdivision hilfreich sein, sofern sich eine Nullstelle durch Probieren finden lässt.

Die Nullstellen der Funktion dritten Grades y = f(x) = 2x³ + 3x² − 5x − 6 sollen durch Polynomdivision errechnet werden. Eine Nullstelle findet man durch Einsetzen von x = −1. Der Wert dieser Nullstelle ist in den Teiler immer mit entgegengesetztem Vorzeichen einzusetzen. Das Polynom f(x) wird somit durch den Ausdruck (x + 1) dividiert.

Das Ergebnis der Polynomdivision ist eine quadratische Gleichung. Sie wird in die p-q–Form umgewandelt und Null gesetzt. Die Nullstellen errechnen sich nach Anwenden der p-q–Formel. Die Beispielfunktion 3.Grades hat mit −1, −2 und +1,5 drei reelle Nullstellen. Im Umkehrschluss kann man bei Kenntnis der Nullstellen daraus die Funktionsgleichung ermitteln. Man bildet die Linearfaktoren (x + Nullstelle), indem zu x der negierte Wert der Nullstelle addiert wird. Die Multiplikation aller Linearfaktoren muss dann wieder die Funktionsgleichung ergeben.

In einem weiteren Beispiel werden die Nullstellen eines Polynoms höherer Ordnung durch Polynomdivision ermittelt. Die Stammfunktion f(x) ist so gewählt, dass die Nullstellen zur Bildung des Divisionsfaktors leicht gefunden werden können.

Die Funktion 5. Ordnung hat fünf reelle Nullstellen bei xN1 = −1, xN2 = +2, xN3 = −2, xN4 = +3 und xN5 = −5.
Der dargestellte Funktionsgraph wurde mit mathematischer Software erstellt.

Horner-Schema

Vereinfachtes Berechnen von Polynomwerten

Zur qualitativen Darstellung eines Funktionsgraphen können mit dem Horner-Schema auf einfache Weise Funktionswerte schnell berechnet werden. Das Verfahren ist nach dem englischen Mathematiker William George Horner (*1786, †1837) benannt, der eine viele Jahrhundert ältere Methode neu entdeckte. Es ersetzt das Potenzieren der Variablen durch mehrfache Multiplikationen und Additionen mit den Koeffizienten. Das ist nicht nur in programmierten Berechnungen von Vorteil. Die Potenzen des Polynomausdrucks werden in absteigender Reihenfolge geschrieben und die Koeffizienten als erste Reihe einer Tabelle notiert. Nicht auftretende Potenzen erhalten den Koeffizienten null. Der Variablenwert f(x), für den das Polynom berechnet werden soll, steht vor der zweiten Zeile. Der erste Koeffizient wird direkt in die dritte Reihe übernommen. Mit f(x) wird schrittweise jeder Wert der dritten Zeile multipliziert und das Ergebnis in die zweite Zeile geschrieben. In der Spalte werden die Werte addiert und das Ergebnis als nächster Wert zur Multiplikation in die dritte Zeile geschrieben. Das folgende Beispiel veranschaulicht den Vorgang für mehrere Variablenwerte.

Das Horner-Schema zur Nullstellenbestimmung

Die Bestimmung von Nullstellen kann alternativ zur Polynomdivision mithilfe des Horner-Schemas erfolgen. Zur Ermittlung muss eine Nullstelle bekannt sein oder erraten werden. Das Polynom ab 3. Grad wird geordnet nach absteigenden Potenzen geschrieben, wobei man fehlende Potenzen mit dem Koeffizienten 0 einfügt. Der Term, durch den das Polynom geteilt werden soll, muss in der Form (x±a) vorliegen, wobei a der mit −1 multiplizierte Wert der Nullstelle ist. Das Horner-Schema reduziert das gegebene Polynom um eine Potenz. Bis hierhin ist es mit der Polynomdivision identisch.

Das Horner-Schema kann wieder in Form einer dreizeiligen Tabelle geschrieben werden. Im ersten Schritt wird das Polynom nach Potenzen geordnet geschrieben und durch Nullsetzen versucht eine Nullstelle zu erraten. Im zweiten Schritt werden alle Koeffizienten mit ihren Vorzeichen in eine Reihe geschrieben. Die gefundene Nullstelle steht in der zweiten Zeile links vor den Spalten der Koeffizienten und der Rest der Spalten bleibt vorerst leer. Soll eine Polynomfunktion durch einen gegebenen Linearfaktor geteilt werden, dann wird sein lineares Glied mit −1 multipliziert an den Anfang der zweiten Zeile in das Horner-Schema geschrieben.

Der erste Koeffizient wird unverändert in die dritte Zeile übernommen. Im 3. Schritt wird der Wert der Nullstelle mit dem ersten Koeffizienten multipliziert und das Ergebnis in die noch leere nächste Spalte der zweiten Zeile eingetragen. Die beiden Spaltenwerte werden addiert und das Ergebnis in die dritte Zeile geschrieben. Dieser 3. Schritt wird mit jedem neuen Ergebnis für jede folgende Spalte wiederholt. Im 4. Schritt werden die Ergebnisse der dritten Zeile als Koeffizienten der neuen um eine Potenz niedrigere Polynomfunktion geschrieben.

Bei einer Nullstelle ergibt der letzte Wert in der dritten Zeile immer null. Um weitere Nullstellen zu finden, kann die Methode wiederholt angewendet werden. Da es sich um Polynomfunktion aus dem Abschnitt zur Polynomdivision handelt, kann das Horner-Schema recht einfach für weitere Nullstellen angewendet und überprüft werden.

Polynomzerlegung und Horner-Schema

Das Horner-Schema beruht auf dem kontinuierlichen Ausklammern der Variablen x aus der Polynomfunktion. Das Ergebnis ist eine Reihe additiv verknüpfter Linearfaktoren. Mit jedem Ausklammern verringert sich die Potenz der Variablen x um eins. Fehlende Potenzen in der Polymerfunktion sind in die Normalform mit dem Koeffizienten 0 einzufügen. Die Methode wird im folgenden Beispiel allgemein und am zuvor behandelten Polynom zur Nullstellenbestimmung gezeigt.