Grafisches Ableiten mathematischer Funktionen

Die grafische Darstellung von Funktionen im rechtwinkligen Achsenkreuz ist intuitiv einfach zu verstehen. Mit einem selbst gewählten Wertebereich wird der interessierende Ausschnitt einer Ausgangsfunktion bildlich dargestellt. Der nächste Schritt ist die Differenzialrechnung mit Ableitfunktionen, für die es einprägsame Gesetze gibt. Mit ihnen lassen sich Eigenschaften der gesamten Funktion beschreiben, aber der Zusammenhang ist vielleicht nicht sogleich erkennbar. Sind die Ableitungen oder bestimmte Eigenschaften einer Ausgangsfunktion bekannt, kann damit rückwirkend auch der Verlauf der Ausgangsfunktion dargestellt werden. Vor dem theoretischen Teil der Differenzialrechnung kann mit 'Malen nach Zahlen', dem grafischen Ableiten, der Zugang zum Thema erleichtert werden.

Nullstellen und y-Achsenabschnitt

Ohne grafisches Ableiten lassen sich aus dem Funktionsbild bei geschickter Wahl des Wertebereichs schon charakteristische Punkte der gegebenen Funktion erkennen. Nur mit der Ausgangsfunktion können Schnitt- oder Berührpunkte des Funktionsbilds mit der x-Achse, Nullstellen genannt und ein Schnittpunkt mit der y-Achse bestimmt werden. Für jede Nullstelle gilt, dass der Funktionswert f(xo) = 0 ist. Die Bestimmungsgleichung ist dann nur noch von xo abhängig und kann berechnet werden. Für den y-Achsenabschnitt gilt, dass in der Funktion immer die Variable x = 0 ist. Da der Funktionswert f(x=0) = y ist, muss die gesuchte y-Komponente gleich dem absoluten Glied der Funktion sein, da zur Bestimmung alle mit x behafteten Glieder null gesetzt werden.

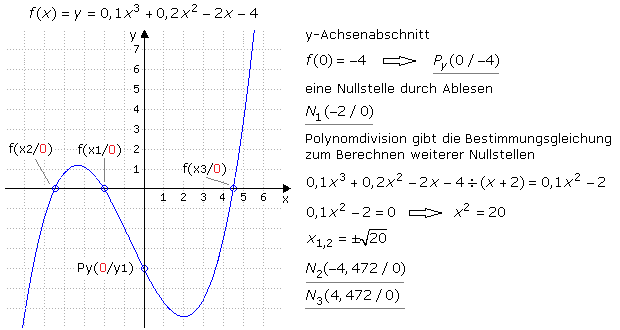
Steigungsfunktion, 1. Ableitung

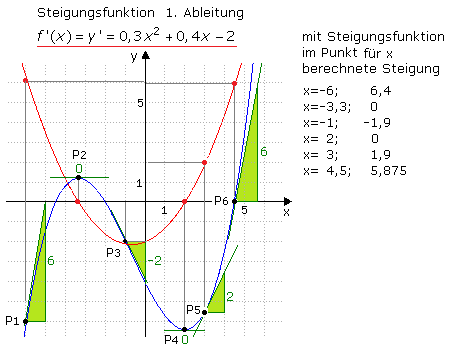
Der Begriff der Steigung sollte verstanden sein. Es handelt sich um den Winkel, den eine Gerade im rechtwinkligen Achsenkreuz zur horizontalen Richtung, der x-Achse, hat. Eine Gerade hat in jedem Punkt die gleiche Steigung, die man durch das Achsenverhältnis Δy / Δx errechnen kann. Der Steigungswinkel φ folgt mathematisch mit arctan(φ) des Achsenverhältnisses. Eine beliebige Kurve kann in jedem Kurvenpunkt eine andere Steigung haben.

Für die blaue Ausgangsfunktion wird für die Kurvenpunkt P1 bis P6 die Steigung grafisch mithilfe einer Tangente bestimmt. Sie ist eine Gerade, die den Kurvenpunkt berührt und die Kurve nicht schneidet. Ihre Steigung wird bestimmt, indem man vom Punkt eine Einheit, dem x-Achsenabschnitt nach rechts und dann vertikal nach oben oder unten geht, bis man auf die Tangente trifft. Diese Strecke ist der y-Achsenabschnitt, der im Verhältnis zum x-Achsenabschnitt die Steigung im gewählten Kurvenpunkt angibt. Für die Punkte P2 und P4 ist der y-Achsenabschnitt null und folglich die Steigung 0. Wird dieser Vorgang für viele Kurvenpunkte wiederholt und in einem neuen Achsenkreuz mit gleicher Achsenteilung (oder dem gleichen Achsenkreuz) eingetragen, dann ist die Verbindung aller Punkte die Steigungsfunktion. Für das gewählte Beispiel ist es die rote Parabel und mathematisch mit f'(x) die 1. Ableitung der Ausgangsfunktion. Mit der Steigungsfunktion kann für jeden beliebigen Punkt der Ausgangsfunktion die Steigung bestimmt werden, wenn für einen x-Wert auf der roten Kurve der zugehörige y-Wert abgelesen wird.

Beim Betrachten beider Funktionsgraphen fällt auf, dass die Steigungsfunktion (rot) dort ihre Nullstellen hat, wo die Ausgangsfunktion (blau) ein lokales Maximum oder ein lokales Minimum hat. Diese Punkte werden allgemein als relative Extrempunkte bezeichnet. Im Beispiel ist der Punkt P2 das relative Maximum oder der Hochpunkt und der Funktionsgraph durchläuft eine Rechtskrümmung. Der Punkt P4 auf der Ausgangsfunktion ist das relative Minimum oder der Tiefpunkt und der Funktionsgraph durchläuft eine Linkskrümmung. In jedem Hoch- oder Tiefpunkt ist die Steigung immer null.

2. Ableitung

Im Beispiel hat die Ausgangsfunktion f(x) (blau) als Steigungsfunktion die Parabel f'(x) (rot) mit zwei Nullstellen und einem Tiefpunkt. Wird sie als neue Ausgangsfunktion g(x) betrachtet, kann auch für sie grafisch das Steigungsverhalten mithilfe von Tangentensteigungen ermittelt werden. Eingezeichnet ist das für die Punkte P1 bis P5. Die Verbindung der zugehörigen neuen Punkte (grün) ist die Steigungsfunktion g'(x) und gleichzeitig die 2. Ableitung f''(x) der Ausgangsfunktion f(x).

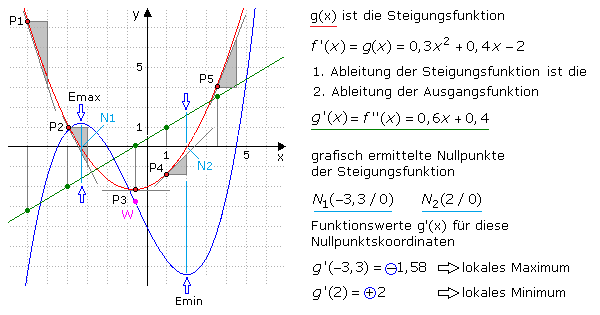
Die x-Koordinate jeder Nullstelle der 1. Ableitung wird in die 2. Ableitung der Ausgangsfunktion eingesetzt und der Funktionswert berechnet. Ist das Ergebnis negativ, dann hat die Ausgangsfunktion f(x) an dieser x-Koordinate einen Hochpunkt, bei positivem Ergebnis einen Tiefpunkt.

Mittig zwischen den Nullstellen der 1. Ableitung liegen ihre lokalen Extrempunkte. Ihre x-Koordinaten bestimmen auf der Ausgangsfunktion die Lage der Wendepunkte. Es ist zu erkennen, dass zwischen einem Hoch- und Tiefpunkt sich der Krümmungsverlauf von einer Rechts- in eine Linkskurve ändert. Der Wendepunkt ist ein charakteristischer Punkt einer Ausgangsfunktion, der mithilfe ihrer 2. Ableitungen bestimmt wird, wobei der Wert entweder positiv oder negativ ist.

Wendepunkt oder Sattelpunkt

Nur wenn die 1. Ableitung einen Hoch- oder Tiefpunkt hat, kann die 2. Ableitung null gesetzt werden. Die daraus folgende x-Koordinate wird in die Ausgangsfunktion eingesetzt und ihr Funktionswert bestimmt die y-Koordinate des Wendepunkts. Im Beispiel ist der Punkt P3 der Tiefpunkt der 1. Ableitung. Seine x-Koordinate kann zu xw = −0,66 abgelesen werden. Der Funktionswert f(xw) errechnet sich damit zu yw ≈ −2,6. Der Wendepunkt (violett) liegt im Koordinatensystem abgelesen bei W(−0,66 / −2,6).

Die 2. Ableitung von f(x) ist die grüne Gerade und kann ein weiteres Mal abgeleitet werden. Für die Ausgangsfunktion f(x) ist die 3. Ableitung mit f'''(x) = 0,6 konstant und ungleich null. Es ist eine horizontal zur x-Achse verlaufende Gerade. Die Bedingung für einen Wendepunkt ist also f''(xo) = 0 und f'''(xo) ≠ 0. Der positive Wert der 3. Ableitung gibt den Richtungswechsel im Wendepunkt von rechts nach links an.

Ist die erste und die zweite Ableitung einer Ausgangsfunktion für eine bestimmte x-Koordinate null und die dritte Ableitung für diesen x-Wert ungleich null, so liegt ein Wendepunkt mit waagerechter Tangente vor. Dieser spezielle Wendepunkt wird als Sattelpunkt oder Terrassenpunkt bezeichnet. In der 1. Ableitung fallen Nullstellen und relative Extrempunkte zusammen.

Monotonie und Krümmungsverhalten

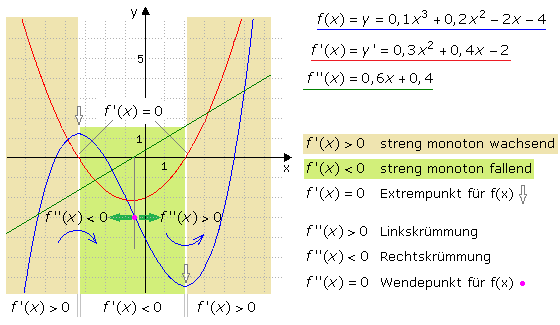
Die Ausgangsfunktion soll im gesamten Definitionsbereich differenzierbar sein. Wie zuvor gezeigt wurde, bestimmt die 1. Ableitung das Steigungs- und damit das Monotonieverhalten der Funktion. Im Bereich aller x-Werte für die f'(x) > 0 gilt ist die Steigung streng monoton wachsend. Im Bereich der x-Werte mit f'(x) < 0 verhält sich die Funktion streng monoton fallend. Bei strenger Monotonie darf die 1. Ableitung nicht null werden. Gilt im Intervall x für f'(x) ≥ 0, so ist das Verhalten der Ausgangsfunktion monoton wachsend, mit f'(x) ≤ 0 monoton fallend.

Mit der 2. Ableitung kann für jeden x-Wert das Krümmungsverhalten der Ausgangsfunktion bestimmt werden. Ist der Funktionswert mit f''(x) > 0 positiv so liegt an dieser Stelle eine Linkskrümmung vor. Ist der Funktionswert mit f''(x) < 0 negativ, so besteht an dieser Stelle eine Rechtskrümmung. Ist der Funktionswert f''(x) > 0, so hat die Ausgangsfunktion einen Wende- oder Sattelpunkt.

Notwendige und hinreichende Bedingungen

In der Mathematik werden die beiden Eigenschaften strenger ausgelegt als im gewohnten Sprachgebrauch. In der Kurvendiskussion beschreiben beide Begriffe die Voraussetzungen, die erfüllt sein müssen, um beispielsweise eindeutig einen Extrempunkt als Hoch- oder Tiefpunkt oder einen Wendepunkt als Sattelpunkt zu benennen. Der Begriff hinreichend kann vielleicht besser verständlich und gleichberechtigt durch ausreichend ersetzt werden. Es soll der Zusammenhang oder die Abhängigkeit von den Aussagen A und B betrachtet werden. Mathematisch wird als Symbol ein Pfeil geschrieben. Bei der Implikation (Einbeziehung) zeigt der Pfeil nur in eine Richtung. Bei der Äquivalenz in beide Richtungen. Dieser Folgepfeil kann auch als wenn ... dann umschrieben werden.

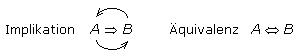
Der Folgepfeil der Implikation steht für die Aussage: Wenn A wahr ist, dann ist B wahr. Die Umkehrung ist nicht zwangsläufig gegeben. Die Eigenschaft von A ist hinreichend für B oder A muss wahr sein, damit B wahr wird. Von B in Richtung A betrachtet ist seine Eigenschaft notwendig für A, da B nur dann wahr ist, wenn auch A wahr ist. Andere denkbare Möglichkeiten, die B wahr werden lassen, kann es geben, sind aber in dieser Betrachtung nicht vorgesehen. Damit ist die hinreichende Eigenschaft von A für B stärker als die notwendige Eigenschaft von B für A.

Der spezielle Fall der Äquivalenz erfüllt gleichermaßen beide Richtungen. Die Eigenschaft von A ist notwendig und hinreichend für die Eigenschaft von B und umgekehrt ist die Eigenschaft von B notwendig und hinreichend für die Eigenschaft von A. Bei einer mathematisch korrekten Umwandlung von Termen ist die Äquivalenz erfüllt. Zwischen beiden Termen kann ein Gleichheitszeichen geschrieben werden.

Die grafischen Ableitungen zeigen, welche Eigenschaften notwendig und hinreichend für bestimmte Kurvenpunkte sind. Die Ausgangsfunktion soll mehrfach ohne Einschränkungen differenzierbar sein. Im relativen Extremwert ist die Steigung null. Die 1. Ableitung hat als Steigungsfunktion an ihren Nullstellen den Funktionswert null. Bei diesen xo-Werten hat die Ausgangsfunktion die Steigung null. Das gilt auch für einen Sattelpunkt, der kein relatives Maximum oder Minimum der Ausgangsfunktion ist. Für relative Extremwerte muss zusätzlich die Eigenschaft f''(xo) ≠ 0 erfüllt sein.

Hinreichend für einen Hochpunkt

Die Ausgangskurve besitzt in xo eine waagerechte Tangente und Rechtskrümmung. Es gilt f'(xo) = 0 und f''(xo) < 0.

Hinreichend für einen Tiefpunkt

Die Ausgangskurve besitzt in xo eine waagerechte Tangente und Linkskrümmung. Es gilt f'(xo) = 0 und f''(xo) > 0.

Vollkommen hinreichend (ausreichend) sind diese beiden Kriterien noch nicht, denn die 2. Ableitung könnte auch null sein und die Ausgangskurve hat bei xE einen relativen Extrempunkt. Es müssen weitere Ableitungen existieren, die dann an der Stelle f'(xE) = 0 zu untersuchen sind. Mit der nächstfolgenden, nichtverschwindenden Ableitung sind allgemeine Aussagen für Extrempunkte möglich.

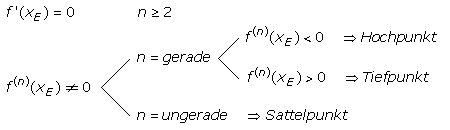
Das folgende Beispiel zeigt die Anwendung für ein Polynom vierter Ordnung. An der Stelle xE ist die Steigung null. Die geradzahlige 4. Ableitung ist ungleich null und positiv. Die Ausgangsfunktion hat an dieser Stelle einen (absoluten) Tiefpunkt.

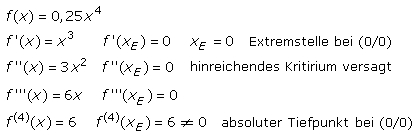
Die Ausgangsfunktion hat Wendestellen, zu denen auch Sattelpunkte zählen. An diesen Stellen hat die Steigungsfunktion Extrempunkte und die 2. Ableitung Nullstellen. Die Ausgangsfunktion muss mehrfach ableitbar sein. Im Sattelpunkt ist die Steigung null, daher muss auch die 1. Ableitung null sein.

Hinreichend für einen Wendepunkt

Die 2. Ableitung hat mit f''(xo) = 0 Nullstellen und dort ist f'''(xo) ≠ 0.

Hinreichend für einen Sattelpunkt

Die 1. Ableitung hat mit f'(xo) = 0, Nullstellen und dort ist f''(xo) = 0 und f'''(xo) ≠ 0.