Der Reihenschwingkreis

Eine Reihenschaltung aus Wirkwiderstand R, Kondensator C und Spule L besitzt mit C und L zwei sich gegenseitig ergänzende Energiespeicher. Der Kondensator speichert elektrische und die Spule magnetische Energie, die sich im gemeinsamen Stromkreis gegenseitig umwandeln kann. Bei Blindwiderständen sind Strom und Spannung gegeneinander um 90° phasenverschoben. Im Strommaximum ist der Kondensator entladen und das Magnetfeld der Spule hat die maximale Feldstärke erreicht. Das Magnetfeld baut sich im weiteren Verlauf ab und lässt den elektrischen Strom in gleicher Richtung durch die Schaltung fließen in die er Beim Feldaufbau geflossen ist. Dieser Strom lädt den Kondensator in umgekehrter Polarität neu auf. Der Prozess setzt sich periodisch umgekehrt fort. Die Schaltung führt freie Schwingungen aus, bis die einmal zugeführte Energie am Wirkwiderstand als Wärmeleistung abgegeben worden ist.

Ein mit L und C gleich dimensionierter Reihen- und Parallelschwingkreis hat dieselbe Resonanzfrequenz, sodass die Schwingungsformel nach Thomson zur Berechnung für beide unverändert gilt. Wird der Reihenschwingkreis an einer Konstantspannungsquelle variabler Frequenz betrieben, kann der Amplituden- und Phasenfrequenzgang messtechnisch aufgenommen werden. Die Impedanz des Schwingkreises ist von der anliegenden Signalfrequenz abhängig und beeinflusst den Kreisstrom.

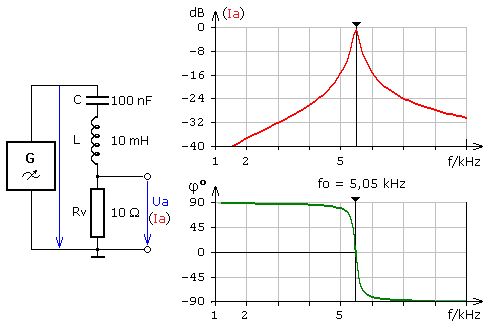
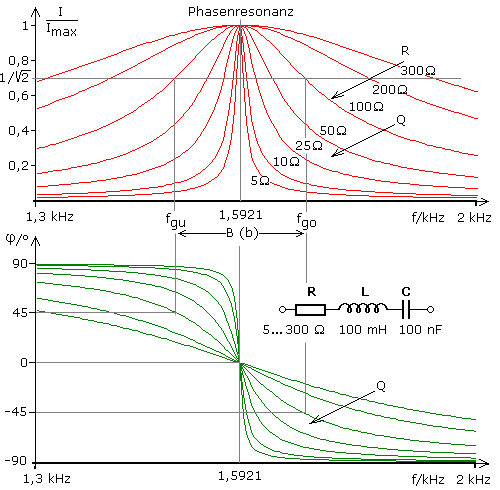
Ein Oszilloskop ist ein Spannungsmessgerät, daher ist in der Schaltung der Widerstand Rv als Stromäquivalent notwendig. Im realen Schwingkreis hat die Spule ihren in Reihe liegenden Drahtwiderstand. Mit einem zusätzlichen Vorwiderstand können bei Bedarf die Schwingkreisgüte und die Bandbreite verändert werden. Die folgende Grafik zeigt den Einfluss des WirkwWiderstands auf die Eigenschaften des Schwingkreises. Je kleiner sein Wert ist, desto ausgeprägter und steiler ist der Kurvenverlauf im Bereich der Resonanzfrequenz. Die Kreisgüte Q ist das Verhältnis aus dem Blindwiderstand zum Wirkwiderstand und nimmt mit kleinerem Wirkwiderstand zu. Die Resonanzfrequenz ist von der Güte unabhängig. Für R = 100 Ω ist die absolute Bandbreite B zwischen φ = ±45° mit eingezeichnet. Mit zunehmender Güte nimmt die Bandbreite ab.

In einer Reihenschaltung ist der durch alle Bauteile gleich große Strom die Bezugsgröße. Ihm wird der Phasenwinkel φ = 0° zugeordnet. Strom und Spannung am Wirkwiderstand sind mit φ = 0° in Phase. Die Spannung am Kondensator ist um φ = −90° und an der Induktivität um φ = +90° zum Strom phasenverschoben. Damit kann das Zeigerdiagramm der RLC-Reihenschaltung gezeichnet und ausgewertet werden. Nur die beiden Blindwiderstände sind von der Frequenz abhängig. Alle Teilspannungen sind direkt proportional zu den Widerstandswerten der Bauteile.

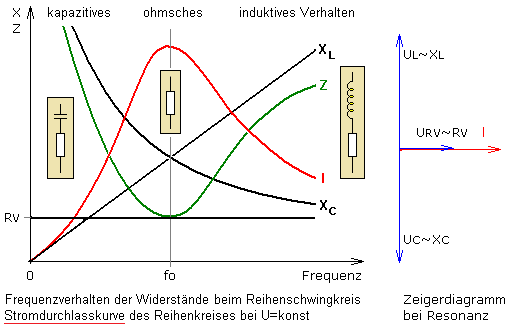
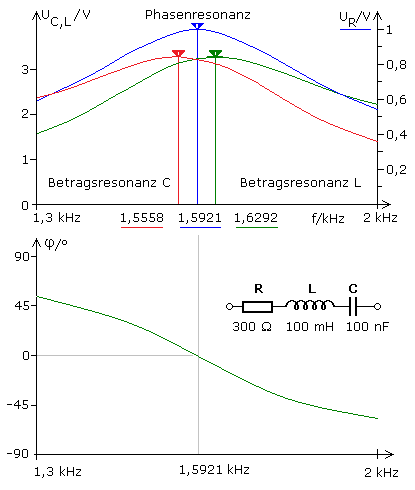
Das weiter oben dargestellte Phasendiagramm zeigt, dass bei der Resonanzfrequenz der Winkel φ = 0° beträgt. Nach außen verhält sich die Schaltung in Bezug auf Spannung und Strom wie ein Wirkwiderstand. Das bedeutet im Resonanzfall haben beide Blindwiderstände den gleichen Wert. Im Zeigerdiagramm bilden sie zueinander den Winkel von 180° und heben sich nach außen hin in ihrer Wirkung gegenseitig auf. Unterhalb der Resonanzfrequenz ist der kapazitive Blindwiderstandswert größer und der Reihenschwingkreis entspricht dort mehr einer RC-Reihenschaltung und zeigt kapazitives Verhalten. Oberhalb der Resonanzfrequenz mit größerem induktivem Blindwiderstand entspricht er eher einer RL-Reihenschaltung mit induktiven Verhalten. Im Resonanzfall wird die Impedanz nur vom normalerweise sehr niederohmigen Drahtwiderstand der Spule bestimmt und durch die Schaltung fließt ein hoher maximaler Resonanzstrom.

Der folgende Videoclip zeigt, welchen Einfluss im Reihenschwingkreis die einzelnen Bauteile haben. Eine individuelle Steuerung ist nur mit der einblendbaren Controlleiste möglich. Als erster Parameter ändert sich der Wert des Wirkwiderstands. Dabei kann es sich um einen zusätzlichen Reihenvorwiderstand handeln oder um Spulen gleicher Induktivität mit unterschiedlichen Drahtwiderständen. Je kleiner dieser Widerstandswert ist, desto steiler verläuft die Resonanzkurve zur Resonanzstelle, wobei sich die Bandbreite verringert und die Schwingkreisgüte zunimmt. Zusätzlich bestimmt auch das Verhältnis von L und C die Kreisgüte. Eine festgelegte Resonanzfrequenz kann durch unterschiedliche L/C-Kombinationen erreicht werden. Die Impedanzkurve (im Video die rote Z-Kurve) ist bei größerem L und kleinerem C schmaler und die Kreisgüte besser.

Bei Resonanz sind die Werte beider Blindwiderstände gleich groß und wesentlich größer als der nach außen hin wirksame Drahtwidertstand R der Spule. Im Zeigerdiagramm liegen die Blindwiderstandszeiger auf der Imaginärwertachse zueinander im Winkel von 180°. Sie heben sich bei gleicher Länge in ihrer Wirkung nach außen hin auf. Bei Resonanz bleibt nur der kleine Widerstandszeiger auf der horizontalen Realwertachse wirksam und bestimmt den maximalen Resonanzstrom. Er fließt in der Reihenschaltung von R, L und C durch alle Bauteile und führt an einem ausgewählten Blindwiderstand beim Reihenschwingkreis zur Spannungsüberhöhung. In einer praktischen Schaltung müssen die Isolationen im Kondensator und der Spule über eine ausreichend hohe Spannungsfestigkeit verfügen.

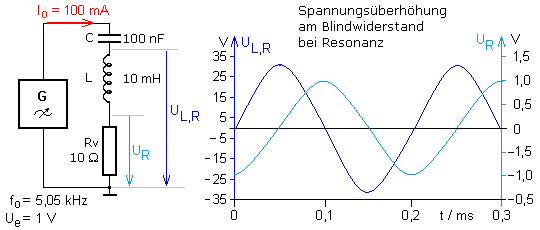
Diese Spannungsresonanz des Reihenschwingkreises kann in der Signalverarbeitung genutzt werden. Die am Blindwiderstand angeschlossene Folgestufe darf diese Resonanzspannungsquelle nicht belasten und muss daher eine sehr hohe Eingangsimpedanz haben. Als Folgestufe eignet sich ein nicht invertierender Operationsverstärker oder eine Transistorstufe in der Kollektorgrundschaltung.

Bei einem Schwingkreis geringerer Güte zeigt das Simulationsergebnis, dass die Spannungsmaxima an den Blindwiderständen nicht mehr bei der Resonanzfrequenz und dem Phasenwinkel φ = 0° messbar sind. Für die gewählte Dimensionierung liegt die Resonanzfrequenz bei 1,592 kHz. Die Güte hat den Wert Q = 3,33. Für den Resonanzfall haben die Blindwiderstände den Wert 1 kΩ

Mathematische Herleitungen

Impedanzgleichung mithilfe der normierten Frequenz

Für einen Schwingkreis ist die Resonanzfrequenz ein charakteristischer Wert. In vielen wissenschaftlichen Veröffentlichungen wird auf diesen Wert normiert. Die normierte Kreisfrequenz Ω ist mathematisch die aktuelle Kreisfrequenz dividiert durch den Wert der Resonanzkreisfrequenz. Die Herleitungen erfolgen mit komplexer Rechnung. Es wird mit der idealisierten Resonanzgleichung gerechnet. Es soll gelten: \[\Omega = \frac{\omega }{{{\omega _o}}} = \frac{f}{{{f_o}}}\quad \quad {\omega _o} = \frac{1}{{\sqrt {L\,C} }}\] Die Impedanzgleichung wird aufgestellt, mit \({\omega _o}/{\omega _o}\) erweitert und umgeformt: \[\begin{array}{l} \underline Z = R + j\,\omega \,L + \frac{1}{{j\,\omega \,C}}\\ \underline Z = R + j\,\Omega \,L\,{\omega _o} + \frac{1}{{j\,\Omega \,C\,{\omega _o}}} \end{array}\] R ausklammern und \({\omega _o}\) ersetzen ergibt: \[\underline Z = R\left[ {1 + j\,\Omega \frac{L}{R}\frac{1}{{\sqrt {L\,C} }} + \frac{{\sqrt {L\,C} }}{{j\,\Omega \,R\,C}}} \right]\] Die beiden Ausdrücke können ersetzt werden durch: \[\frac{L}{{\sqrt {L\,C} }} = \sqrt {\frac{L}{C}} \quad \quad \frac{{\sqrt {L\,C} }}{C} = \sqrt {\frac{L}{C}} \] In die Formel zuvor eingesetzt und mit der Kreisgüteformel verbunden ergibt sich: \[\begin{array}{l} \underline Z = R\left[ {1 + j\,\Omega \frac{{\sqrt {L/C} }}{R} + \frac{{\sqrt {L/C} }}{{j\,\Omega \,R}}} \right]\quad \quad Q = \frac{{\sqrt {L/C} }}{R}\\ \underline Z = R\left[ {1 + j\,\Omega \,Q + \frac{Q}{{j\,\Omega }}} \right] = R\left[ {1 + j\,\Omega \,Q - \frac{{j\,Q}}{\Omega }} \right]\\ \underline Z = R\left[ {1 + j\,Q\,\left( {\Omega - \frac{1}{\Omega }} \right)} \right] \end{array}\]

Bei Resonanz ist Ω = 1 und die Kreisimpedanz wird mit Z = R real und ist gleich dem herkömmlichen Ergebnis. Unterhalb der Resonanzfrequenz wird Ω kleiner. Im Klammerausdruck wird davon der Kehrwert subtrahiert, wodurch das Ergebnis zunehmend negativer wird. Der Schwingkreis zeigt kapazitives Verhalten. Oberhalb der Resonanzfrequenz wird Ω größer und strebt dem größeren positiven Wert von Ω an. Der Schwingkreis zeigt induktives Verhalten.

Bandbreite, Güte und Resonanzwiderstand

Die Stromamplitude hat beim Reihenschwingkreis im Resonanzfall den Maximalwert. Die Grenzfrequenzen liegen bei 70,7...% des Maximalwerts. Die absolute Bandbreite errechnet sich aus der Differenz zwischen oberer und unterer Grenzfrequenz: \[B = \Delta f = {f_{go}} - {f_{gu}}\] Ohne zusätzliche Wirkwiderstände bestimmt der Drahtwiderstand der Spule die Güte der Spule und somit die des Reihenschwingkreises. Der Kondensator hat verglichen zur Spule praktisch ideales Verhalten. Die den Schwingkreis speisende Signalquelle sollte eine Spannungsquelle sein. Ihr Innenwiderstand bildet mit dem Drahtwiderstand eine Reihenschaltung. Die Schwingkreisgüte kann mithilfe der folgenden Rechnung universeller bestimmt werden: \[\begin{array}{l} Q = \frac{{{X_L}}}{{{R_V}}} = \frac{{2\,\pi \,{f_o}\,L}}{{{R_V}}}\quad \quad {f_o} = \frac{1}{{2\,\pi \,\sqrt {L\,C} }}\\ Q = \frac{L}{{{R_V}\,\sqrt {L\,C} }}\quad \Rightarrow \quad Q = \frac{1}{{{R_V}}}\sqrt {\frac{L}{C}} \quad \end{array}\]

Für eine gewünschte Resonanzfrequenz können nach der Thomson-Schwingungsgleichung mathematisch viele Variationen von L und C genutzt werden. Für Schwingkreise hoher Güte sind bei gleichem Rv nur Bauteilkombinationen hoher Induktivität und kleiner Kapazität möglich.

Wird das Signal parallel zum Reihenschwingkreis als neues Quellensignal genutzt, dann arbeitet der Schwingkreis als Frequenzfalle, auch Traps oder Kerbfilter genannt. In einem engen Frequenzband um die Resonanzfrequenz herum ist er niederohmig, hat eine kleine Ausgangsspannung und filtert diesen Frequenzbereich aus. Bilden der Reihenschwingkreis und die Folgestufe eine Serienschaltung, dann wirkt er als Saugkreis und lässt als Eintor niedriger Impedanz bevorzugt nur den schmalbandigen Frequenzbereich durch. In Abstimmkreisen kann auch die Spannungsüberhöhung an C oder L direkt ausgewertet werden, wenn die Folgestufe mit einer sehr hohen Eingangsimpedanz den Reihenschwingkreis vernachlässigbar belastet. Die wichtigsten Eigenschaften eines Reihenschwingkreises sind:

Bei Resonanz wirkt ein Reihenschwingkreis wie ein Wirkwiderstand.
Die Impedanz des Reihenkreises hat bei Resonanz ihren kleinsten Wert.
Bei der Resonanzfrequenz fließt in und durch den Kreis der maximale Strom.
Durch Resonanzüberhöhung sind an den Blindwiderständen die Spannungen viel höher als die anliegende Quellenspannung.
Ohne zusätzlichen Vorwiderstand wird die Kreisgüte vom Drahtwiderstand der Spule bestimmt.
Die Bandbreite ist umgekehrt proportional zur Kreisgüte.
Die Resonanzfrequenz ist unabhängig vom Wert des Verlustwiderstands.

Herleitung der Grenzfrequenzgleichungen

Die charakteristischen Werte eines Schwingkreises sind seine Resonanzfrequenz und die Grenzfrequenzen. Sie können experimentell einfach bestimmt werden, ebenso aber auch berechnet werden. Bei jeder Grenzfrequenz ist per Definition der absolute Phasenwinkel φ = 45° und der Wert des Blindwiderstands ist gleich dem des realen Wirkwiderstands. Das Vorzeichen wird durch den mehr induktiven oder kapazitiven Charakter der Schaltung bestimmt. Mit diesem Ansatz lassen sich die Bestimmungsgleichungen der Grenzfrequenzen herleiten.

Lösungsansatz für die untere Grenzfrequenz: \[\begin{array}{l} R = \frac{1}{{{\omega _{gu}}\,C}} - {\omega _{gu}}\,L\quad \Rightarrow \quad {\omega _{gu}}\,C\,R = 1 - \omega _{gu}^2\,L\,C\\ \omega _{gu}^2\,L\,C + {\omega _{gu}}\,C\,R = 1\quad \Rightarrow \quad \omega _{gu}^2 + {\omega _{gu}}\frac{R}{L} = \frac{1}{{L\,C}} \end{array}\] Mit der Resonanzfrequenz \({\omega _o} = 1/\sqrt {L\,C} \) angewendet auf die rechte Seite entsteht die quadratische Gleichung: \[\omega _{gu}^2 + {\omega _{gu}}\frac{R}{L} = \omega _o^2\] Sie wird mithilfe der quadratischen Ergänzung und der p-q-Formel gelöst: \[\begin{array}{l} {\omega _{gu}} = - \frac{R}{{2\,L}} \pm \sqrt {\omega _o^2 + {{\left( {\frac{R}{{2\,L}}} \right)}^2}} \\ {f_{gu}} = \frac{1}{{2\,\pi }}\left[ {\sqrt {\omega _o^2 + {{\left( {\frac{R}{{2\,L}}} \right)}^2}} - \frac{R}{{2\,L}}} \right] \end{array}\] Die Herleitung für die obere Grenzfrequenz erfolgt entsprechend mit positivem \(R/2\,L\): \[{f_{go}} = \frac{1}{{2\,\pi }}\left[ {\sqrt {\omega _o^2 + {{\left( {\frac{R}{{2\,L}}} \right)}^2}} + \frac{R}{{2\,L}}} \right]\]

Die mathematische Herleitung zeigt die Abhängigkeit der Bandbreite von der Schwingkreisgüte. Die Grenzfrequenzformeln werden in die Bandbreitenformel eingesetzt und umgeformt: \[B = {f_{go}} - {f_{gu}}\quad \Rightarrow \quad B = \frac{R}{{2\,\pi \,L}} = \frac{{R\,{f_o}}}{{{X_o}}}\] Dämpfung d und Güte Q sind zueinander reziprok. Die Güte ist der Quotient aus Blindkomponente zur Realkomponente. \[\begin{array}{l} d = \frac{1}{Q}\quad mit\quad Q = \frac{X}{R} = \frac{{2\,\pi \,{f_o}\,L}}{R}\\ d = \frac{R}{X} = \frac{R}{{2\,\pi \,{f_o}\,L}}\quad \Rightarrow \quad \frac{R}{L} = 2\,\pi \,{f_o}\,d = {\omega _o}\,d \end{array}\] R/L in den Grenzfrequenzformeln ersetzen führt über einige Zwischenschritte zu: \[\begin{array}{l} {f_{gu,go}} = \frac{1}{{2\,\pi }}\left[ {\sqrt {\omega _o^2 + \omega _o^2{{\left( {\frac{d}{2}} \right)}^2}} \mp \frac{{{\omega _o}\,d}}{2}} \right]\\ {f_{gu,go}} = \frac{1}{{2\,\pi }}\left[ {{\omega _o}\sqrt {1 + {{\left( {\frac{d}{2}} \right)}^2}} \mp \frac{{{\omega _o}\,d}}{2}} \right]\\ {f_{gu,go}} = {f_o}\left[ {\sqrt {1 + {{\left( {\frac{d}{2}} \right)}^2}} \mp \frac{d}{2}} \right] \end{array}\] Werden mit diesen hergeleiteten Formeln die Grenzfrequenzen des zuletzt simulierten Reihenschwingkreises geringer Güte Q = 3,33 berechnet, dann stimmen die Werte der beiden Grenzfrequenzen \({f_{gu}} = 1,371\;kHz\) und \({f_{go}} = 1,849\;kHz\) mit den Ablesewerten der Simulation sehr gut überein. Für Gütewerte Q ≥ 10 ist in der Grenzfrequenzformel der Wert unter der Wurzel nahezu 1. Die Grenzfrequenzen können in guter Näherung durch die folgenden Beziehungen berechnet werden: \[\begin{array}{l} {f_{gu}} \approx {f_o}\,\left( {1 - \frac{d}{2}} \right) = {f_o}\,\left( {1 - \frac{1}{{2\,Q}}} \right)\\ {f_{go}} \approx {f_o}\,\left( {1 + \frac{d}{2}} \right) = {f_o}\,\left( {1 + \frac{1}{{2\,Q}}} \right)\\ \end{array}\]

Beim Reihenschwingkreis liegen die Grenzfrequenzen nahezu symmetrisch zur Resonanzfrequenz. Sie kann aus dem geometrischen Mittel beider Grenzfrequenzen errechnet werden: \[{f_o} = \sqrt {{f_{gu}} \cdot {f_{go}}} \quad \quad {\omega _o} = \sqrt {{\omega _{gu}} \cdot {\omega _{go}}} \]