Der RC-Hochpass als Differenziator
Im Artikel der Tiefpass als Integrierer ist beschrieben, dass besonders dimensionierte RC-Tiefpässe Eingangssignale entsprechend der mathematischen Integration zum Ausgangssignal wandeln. Das entgegengesetzte mathematische Verhalten ist bei richtiger Dimensionierung mit RC-Hochpassschaltungen möglich. Das Ausgangssignal zeigt dann den Verlauf der ersten Ableitung des Eingangssignals. Der RC-Hochpass wird als Differenziator oder (früher) Differenzierer bezeichnet.
Nachfolgend wird das Verhältnis der Zeitkonstante τ in Abhängigkeit zur Frequenz eines rechteckförmigen Eingangssignals mit konstanter Amplitude und dem Tastgrad von 0,5 untersucht. Der RC-Hochpass hat eine umschaltbare Zeitkonstante. Die Ausgangsspannung am Widerstand folgt der zeitlichen Stromänderung während der Ladung und Umladung des Kondensators. Das rechteckförmige Eingangssignal kann als ein zwischen maximaler Spannung und null geschaltetes DC-Signal gesehen werden. Beim ersten Einschalten ist der Kondensator ungeladen, es fließt ein nach der e-Funktion abnehmender Ladestrom. Am Widerstand wird die nach der e-Funktion proportional abnehmende Ausgangsspannung gemessen. Bei konstanter Frequenz bestimmt die Zeitkonstante den Ladeverlauf. In der Impulspause wird der Kondensator mit gleicher Zeitkonstante zum Teil entladen.
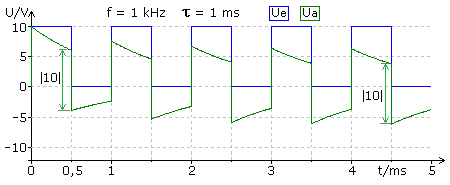
In jeder folgenden Schaltperiode wird von der erreichten Endspannung ausgehend umgeladen. Der Absolutwert der Spannung am Kondensator bleibt gleich und das Ausgangssignal richtet sich symmetrisch zur Nulllinie aus. Das Diagramm zeigt den Vorgang des Einschwingens, der in diesem Beispiel nach 3 ms erreicht ist. Beim unveränderten Eingangssignal ist für sehr kleine Zeitkonstanten der Lade- und Umladevorgang kurz nach dem Einschalten abgeschlossen. Es wird ein nadelförmiges Ausgangssignal messbar, dessen Maximalamplitude von der des Eingangssignals und dem Wert des Wirkwiderstands bestimmt wird.
Die folgende Schaltung zeigt für einen RC-Hochpass mit umschaltbarer Zeitkonstante die Signaldiagramme im sogenannten eingeschwungenen Zustand. Ein Kondensator großer Kapazität wird in den Halbperioden weder vollständig auf- noch entladen. Eine kleinere Kapazität verringert die Zeitkonstante und das Ausgangssignal wird stärker verformt.
| tau = 1,0 ms | tau = 0,47 ms |
| tau = 0,047 ms | tau = 0,01 ms |
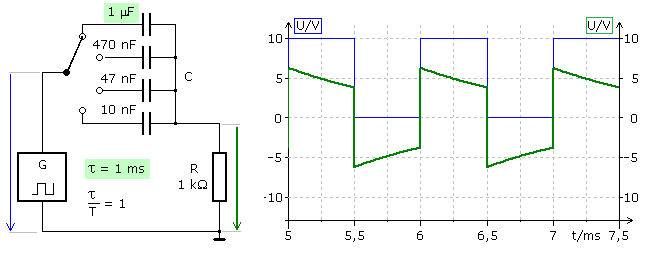
Ist das Verhältnis der Zeitkonstanten τ verglichen mit der Periodendauer T des Eingangssignals sehr klein, so ergeben sich Nadelimpulse am Ausgang. Ein so dimensionierter Hochpass reagiert auf schnelle Eingangsänderungen und wird Differenziator genannt. Ebenso verhält sich ein RL-Hochpass, mit dem Ausgangssignal parallel zur Spule. Soll die Schaltung als RL-Differenziator genutzt werden, muss das Verhältnis der Zeitkonstanten τ = L / R zur Periodendauer T des Eingangssignals sehr viel kleiner als 1 sein.
Im Bild einer Funktion kann für jeden Kurvenpunkt die Steigung durch Anlegen der Tangente an diesen Punkt ermittelt werden. Mathematisch werden die Steigungen mithilfe der ersten Ableitung der Funktionsgleichung und dem Einsetzen des Koordinatenwerts der Abszisse berechnet. Der Vorgang nennt sich Differenzieren. Das vierte Beispiel zeigt den RC-Hochpass als praktisch nutzbaren Differenziator der im Ausgangssignal nur noch schnelle Änderungen des Eingangssignals darstellt.
Der Hochpass als Differenziator
Funktionsgeneratoren bieten nur wenige Signale mit einfachen mathematischen Funktionen, um die Eigenschaft des Differenziators anschaulich darzustellen. Ein Dreiecksignal kann durch zwei Geradengleichungen mit positiver und negativer Steigung beschrieben werden. Die erste Ableitung einer Geradenfunktion ist eine Konstante. Als Ausgangssignal eines Differenziators ist ein Rechtecksignal mit positivem und negativem konstanten Spannungswert zu erwarten. Der Differenzialquotient von sin(x) ergibt cos(x). Die Ableitung einer Parabel führt zu einer linearen Funktion. Die folgende umschaltbare Grafik zeigt für die drei Eingangssignale (blau) nur die qualitativen Ausgangssignale (grün) ohne Angaben zu den Amplituden.
| Dreiecksignal | Sinussignal | Parabelbögen |
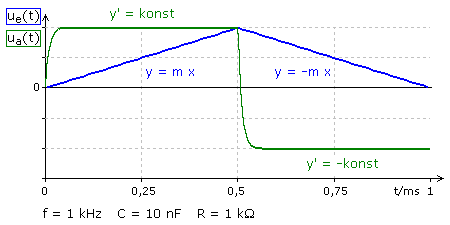
Das parabelförmige Eingangssignal (dünne blaue Linie) wurde durch Integration eines Dreiecksignals generiert. Um die Zuordnung der beiden Parabeln zu ihrer ersten Ableitung hervorzuheben wurden die jeweiligen Parabelbögen (dicke blaue Linie) in das eingezeichnete rechtwinklige Achsenkreuz verschoben.
Anwendungsbeispiele
Vor den Digitalrechnern gab es Analogrechner mit Operationsverstärkern (OPVs) die zusätzlich zu den Grundrechenarten in einem bestimmten Rahmen das Differenzieren und Integrieren ermöglichten. Für mathematisch gute Ergebnisse war zuvor immer ein Abgleich der Schaltung notwendig. In elektronischen Regelschaltungen werden durch zusätzliche Differenziator Schaltungen auch schnelle Änderungen erfasst und können ausgeregelt werden. Bei der Übertragung von Schaltsignalen über mehrere Verstärker oder durch lange Leitungen werden höhere Frequenzanteile stärker gedämpft und die Flankensteilheit geht verloren. Mit Differenziator Schaltungen wird das Tiefpassverhalten ausgeglichen und die Flankensteilheit wieder hergestellt.