Amplitudenmodulation

Jedes Modulationsverfahren versetzt eine zu sendende niederfrequente Information, das Basisband, in einen definierten höheren Frequenzbereich. Das Basisband wird auf ein bestimmtes hochfrequentes Trägersignal moduliert, da nur ausreichend hochfrequente Signale als elektromagnetische Wellen per Funk übertragbar sind. Sollen gleichzeitig mehrere unterschiedliche Informationen drahtgebunden oder optisch durch Glasfaserübertragung übertragen werden, so muss jedes Basisband auf ein eigenes Träger-Sendesignal moduliert werden. Die Sendefrequenzen müssen so weit auseinander liegen, dass sich ihre Modulationsprodukte nicht gegenseitig überlagern. Die gewünschte Information wird durch Auswählen einer Sende- oder Trägerfrequenz aus dem gesamten Sendefrequenzband empfangen und per Demodulation zurückgewonnen. Mit der Amplitudenmodulation (AM) lassen sich viele unterschiedliche Informationen im selben Übertragungsmedium aufeinander folgend gleichzeitig senden. Entlang der Frequenzachse entspricht die Abfolge der modulierten Einzelinformationen einem Frequenzmultiplexverfahren. Dieses Kapitel beschreibt wichtige Aspekte der traditionellen analogen Amplitudenmodulation. Zusätzlich wird in diesem Webprojekt auf einer anderen Seite mit Simulations- und Audiobeispielen das Verhalten sinusförmiger Signale bei der Überlagerung beschrieben.

• Amplitudenmodulation aus mathematischer Sicht
• Die AM mit selektivem Transistorverstärker
• Der Modulationsgrad und die Bandbreite der AM
• Die Leistungsbilanz der AM
• Amplitudenmodulation am Modell der rotierenden Zeiger

Der hochfrequente Träger (HF-Träger) soll einen zeitlich sinusförmigen Verlauf haben und folgt der mathematischen Funktionsgleichung: \[{u_T}(t) = {\widehat u_T} \cdot \cos (\Omega \,t + \varphi )\quad (1)\quad \quad \Omega = 2\,\pi \,{f_T}\] Darin sind \({u_T}(t)\) der Momentanwert und \({\widehat u_T}\) der Spitzenwert der Trägeramplitude. \(2\,\pi \,{f_{T}}\) ist die Träger-Kreisfrequenz. \(\varphi \) ist der Phasenversatz und hat meistens den Wert null.

Die Amplitudenmodulation (AM) war lange Zeit das wichtigste Verfahren um NF-Signale durch Kabel, Rundfunk und analoges Fernsehen zu verbreiten. Die AM ist schaltungstechnisch im Sender und Empfänger einfach zu handhaben. Jede einzelne zu sendende NF-Information in Form von Sprache, Musik oder Bild verändert von den drei möglichen Parametern des HF-Trägers nur die Trägeramplitude, während die Trägerfrequenz und die Phase unbeeinflusst bleiben.

Der Modulator

Wird in der Trägerfunktion Gl.(1) nur der Spitzenwert \({\widehat u_T}\) mit einem größeren oder kleineren Faktor multipliziert, so ändert das nur die Trägeramplitude. Ist der Faktor nicht konstant und folgt einer Sinus- oder Kosinusfunktion mit niedriger Frequenz, so variiert die Trägerfrequenz im Rhythmus der niederfrequenten Information. Mathematisch ist die Modulation eine Multiplikation der HF-Trägerfunktion mit der NF-Informationsfunktion. Die Baugruppe, an der die Rechenoperation erfolgt, wird als Modulator und manchmal als Mischer, im englischen Sprachgebrauch als Mixer bezeichnet. Das modulierende NF-Signal wird oft als Modulationssignal bezeichnet.

Es gibt integrierte Schaltkreise, sogenannte Voll- oder Vierquadranten-Multiplizierer mit getrennten Eingängen für den HF-Träger und das NF-Signal. Das Ausgangssignal des Multiplizierers ist ein spezielles codiertes hochfrequentes AM-Signal. Ausführliche Informationen sind in diesem Webprojekt unter dem Titel AM nach dem Zweiseitenbandverfahren beschrieben. Nachfolgend wird hier die ursprüngliche geträgerte Zweiseitenband AM-Modulation beschrieben. Beide Eingangssignale werden an einer Matrix mit linearen Kennlinien realer Wirkwiderstände additive Überlagert. Das Ausgangssignal ist keine Modulation, da keine neuen Frequenzen entstehen.

Nach der additiven Überlagerung wird das Summensignal einer Baugruppe (Zweitor) mit nicht linearer Kennlinie zugeführt. Sehr gut geeignet ist die Basis-Emitter-Diodenstrecke eines Transistorverstärkers. Das Summensignal soll nur den gekrümmten Kennlinienbereich der leitenden Basis-Emitterdiode aussteuern. Das Ausgangssignal ist stark verzerrt und enthält neue Frequenzen, die im Eingangssignal nicht vorhanden sind. Werden sie mithilfe der Fourieranalyse untersucht, so sind im Frequenzbereich das NF-Basisband und symmetrisch um die einfache und mehrfache ganzzahlige HF-Trägerfrequenz angeordneten die AM-codierten Signale oder Frequenzbänder zu finden.

Shockley-Diodengleichung

Für eine Diodenstrecke kann der Stromfluss des pn-Übergangs idealisiert durch die Shockley-Diodengleichung beschrieben werden. Im Durchlassbereich ist ID der Diodenstrom und UF die Diodenflussspannung. Der Sättigungssperrstrom IS(T) ist von der Temperatur abhängig und liegt bei Si-Dioden im Bereich 10 pA bis 10 μA. Der Emissionskoeffizient n hat ideal den Wert 1 und liegt praktisch zwischen 1 ... 4. Die Spannung UT ist ebenfalls von der Temperatur abhängig und kann mit Naturkonstanten berechnet werden. Bei 20 °C beträgt der Wert rund 25 mV.

Die Shockley-Diodengleichung lautet: \[\begin{array}{l} {I_D} = {I_S}(T) \cdot \left( {{e^{{U_F}/n{U_T}}} - 1} \right)\\ {U_T} = k\,T/q \approx 0,0862 \cdot T\;mV/K \end{array}\] Mit \(k = 1,381 \cdot {10^{ - 23}}\;W\,s/K\) der Boltzmann-Konstante und \(q = 1,602 \cdot {10^{ - 19}}\;A\,s\) der Elementarladung. Mit der Diodenspannung UF größer null und dem absoluten Wert |UF|»UT wird bei Raumtemperatur der Exponentialwert \({e^{{U_F}/n\,{U_T}}} \gg 1\). In guter Näherung gilt für den Durchlassstrom: \[{I_D} \approx {I_s}(T) \cdot \left( {{e^{{U_F}/n\,{U_T}}}} \right)\] Der Exponentialausdruck kann mithilfe der Exponentialreihe geschrieben werden: \[\begin{array}{l} {e^{{U_F}/n\,{U_T}}} = \sum\limits_{n = 0}^\infty {\frac{{{{({U_F}/n\,{U_T})}^n}}}{{n!}}} \quad n! = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n\\ {e^{{U_F}/n\,{U_T}}} = 1 + \frac{{{U_F}}}{{{U_T}}} + \frac{1}{{2!}}{\left( {\frac{{{U_F}}}{{{U_T}}}} \right)^2} + \frac{1}{{3!}}{\left( {\frac{{{U_F}}}{{{U_T}}}} \right)^3} + \frac{1}{{4!}}{\left( {\frac{{{U_F}}}{{{U_T}}}} \right)^4} + \ldots \end{array}\] Im Modulationssignal ist das quadratische Glied klar zu erkennen.

Beim npn-Transistor steuert nur der positive Teil des additiven Überlagerungssignal den gekrümmten Durchlassbereich der Basis-Emitterdiode einer Transistorstufe an. Beide Signalfunktionen werden entsprechend der Potenzreihe multipliziert und führen zum stark verzerrten Ausgangssignal am Kollektor des Transistors. Das ursprüngliche Summensignal ist zu null symmetrisch, steuert aber den Transistoreingang nur mit dem positiven Signalverlauf an. Dem Steuersignal hat somit einen 'Gleichanteil'. Die mathematische Herleitung des AM-Signals wird anschaulicher, wenn zum NF-Signal eine DC-Komponente addiert wird, um es anschließend mit dem Trägersignal zu multiplizieren.

Amplitudenmodulation aus mathematischer Sicht

Die HF-Trägeramplitude hat für jeden Zeitpunkt einen bestimmten Wert. Zum gleichen Zeitpunkt hat die Amplitude des NF-Signals ihren Wert, der als Faktor den zeitlich Wert der Trägeramplitude verändert. Daraus resultiert ein additiver neuer Amplitudenwert für das AM-Signal. Die Ergebniswerte sollen nur positiv oder negativ sein. Die Zeitachse im Zeitdiagramm wird von der HF-Frequenz bestimmt. Zur Vereinfachung sollen die Signale als Kosinusfunktionen gleicher Phasenlage vorliegen. Mathematisch hilfreiche Zusammenhänge zwischen Winkelfunktionen sind im Abschnitt Fachmathematik — Winkelfunktionen erklärt.

Funktionsgleichung des HF-Trägersignals: \[{u_T}(t) = {\widehat u_T} \cdot \cos (\Omega \,t)\quad \quad \Omega = 2\,\pi \,{f_T}\] Funktionsgleichung des NF-Modulationssignals: \[{u_S}(t) = {\widehat u_S} \cdot \cos (\omega \,t)\quad \quad \omega = 2\,\pi \,{f_S}\] Für die Zeitfunktion des AM-Signals gilt: \[{u_{AM}}(t) = ({\widehat u_T} + {\widehat u_T} \cdot {\widehat u_S}\cos (\omega \,t)) \cdot \cos (\Omega \,t)\] Mit dem Modulationsgrad \(m = {\widehat u_S}/{\widehat u_T}\) geschrieben folgt: \[\begin{array}{l} {u_{AM}}(t) = {\widehat u_T}\left( {1 + m \cdot \cos (\omega \,t)} \right) \cdot \cos (\Omega \,t)\\ {u_{AM}}(t) = {\widehat u_T}\,\cos (\Omega \,t) + m\,{\widehat u_T} \cdot \cos (\omega \,t) \cdot \cos (\Omega \,t) \end{array}\] Für das Produkt der Kosinusausdrücke gilt: \[\cos (\omega \,t) \cdot \cos (\Omega \,t) = \frac{1}{2}\cos (\Omega \,t - \omega \,t) + \frac{1}{2}\cos (\Omega \,t + \omega \,t)\] Das Ergebnis nach dem Einsetzen und Umformen lässt das Frequenzspektrum der AM erkennen: \[{u_{AM}}(t) = \frac{{{{\widehat u}_S}}}{2}\cos (\Omega - \omega )\,t + {\widehat u_T}\,\cos (\Omega \,t) + \frac{{{{\widehat u}_S}}}{2}\cos (\Omega + \omega )\,t\] Die Ausdrücke von links nach rechts stehen für das untere Seitenband gefolgt von der Trägerfrequenz und dem oberen Seitenband. Beide Seitenbänder - hier sind es einzelne Frequenzlinien - haben die gleiche Amplitude. Die AM-Funktionsgleichung zeigt, dass nur die Trägeramplitude multipliziert wurde.

Amplitudenmodulation mit selektivem Transistorverstärker

Mit der folgenden einfachen Transistorschaltung wird an der Basis-Emitterdiode eine Amplitudenmodulation durchgeführt. Zur Veranschaulichung ist das Informationssignal eine konstante NF und das Trägersignal eine dazu zeitlich gut auflösbare höhere Frequenz (HF). Beide Signale werden vor der Modulation am Basiswiderstand bei (1) additiv überlagert. Die Signaldiagramme darunter entstanden mit der im Labor erprobten Schaltung mit einem Simulationsprogramm. Für die Messpunkte sind auch die Diagramme der Fourieranalysen dargestellt.

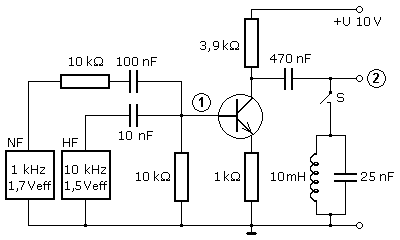
Das additive Überlagerungssignal am Punkt (1) ist zu null symmetrisch und enthält nur die beiden Ausgangsfrequenzen. Der Transistor hat keinen voreingestellten Arbeitspunkt und wird nur von den positiven Signalanteilen des Summensignals angesteuert. Die Amplitude des Summensignals ist im positiven Bereich so groß, dass der gesamte gekrümmte Kennlinienbereich der Basis-Emitterdiode ausgesteuert wird. An dieser Kennlinie wird das Summensignal potenziert. Der Transistor verstärkt die Modulationsprodukte der mehrfachen Multiplikation, die ohne den zugeschalteten Schwingkreis am Punkt (2) messbar sind. Das mittlere Diagrammpaar zeigt das Kollektorsignal nach dem Auskoppelkondensator ohne zugeschalteten Schwingkreis. Im Frequenzspektrum sind neben der NF-Frequenz die AM-Modulation-Seitenfrequenzen symmetrisch angeordnet zur einfachen, doppelten, dreifachen, also dem ganzzahligen Vielfachen der Trägerfrequenz zu erkennen.

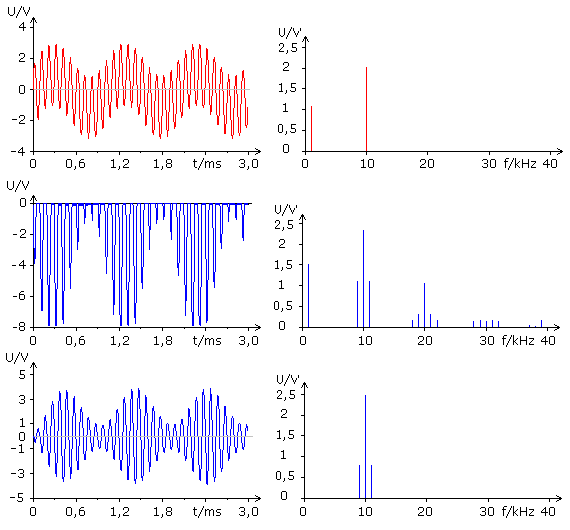
Das gewünschte AM-Signal wird nach der Modulation mit einem auf die einfache Trägerfrequenz abgestimmten Parallelschwingkreis ausreichender Bandbreite ausgefiltert. In der Simulation beträgt die Resonanzfrequenz 10 kHz. Das Frequenzspektrum zeigt nur noch die beiden symmetrisch zum Trägersignal angeordneten Seitenbandsignale. Beide Seitenbänder haben die gleiche Amplitude und können theoretisch bei maximaler Modulation im unverzerrten AM-Signal in der Summe die Amplitude der HF-Trägerfrequenz erreichen. In den Seitenbändern, hier einzelne Frequenzlinien, ist die NF-Information AM codiert (moduliert). Die linke Seitenlinie bei 9 kHz errechnet sich als Differenzfrequenz aus der Trägerfrequenz minus der Informationsfrequenz. Die rechte Seitenlinie mit 11 kHz ist die Summenfrequenz aus der Trägerfrequenz plus der Informationsfrequenz.

In technischen Anwendungen sind die Trägerfrequenzen wesentlich höher. Der analoge Rundfunksendebetrieb für Mittelwelle benutzt HF-Träger zwischen 510 kHz ... 1605 kHz. Im UKW-Sendeband ist das Audio Stereosignal auf 38 kHz und im analogen Fernsehen wurde das Farbartsignal auf eine 4,43 MHz Trägerfrequenz moduliert.

AM-Parameter aus dem Zeitdiagramm

Aus dem Zeitdiagramm eines AM-Signals sind einige Parameter recht einfach zu bestimmen. Immer ist es die konstante Trägerfrequenz und bei einer Einton-AM sind es die Signalfrequenz und der Modulationsgrad. Die Amplitude des Trägers ändert sich symmetrisch im Rhythmus der Informationsfrequenz. Für die NF-Frequenz gibt es keinen geschlossenen Kurvenzug. Sie ist aus der Periodendauer der sogenannten Hüllkurve ablesbar. Sie entsteht als Verbindungslinie der maximalen Amplitudenwerte der modulierten HF-Trägerfrequenz.

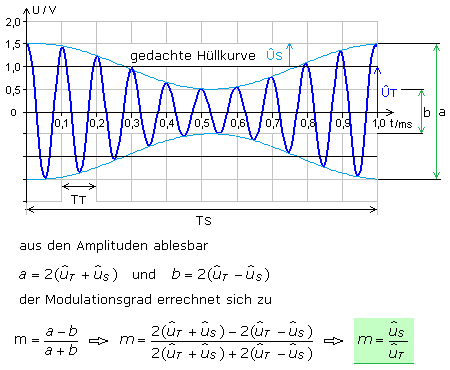
Mit dem Oszilloskop sind im Zeitdiagramm die Seitenfrequenzen nicht zu erkennen. Wird im Zeitdiagramm die maximale und minimale Auslenkung des AM-Signals bestimmt, so kann, wie oben dargestellt, der Modulationsgrad m aus dem Verhältnis der Streckendifferenz zur Streckensumme errechnet werden. Die Strecken a und b sind aus den Amplituden ablesbar: \[a = 2\,({\widehat u_T} + {\widehat u_S})\quad \quad b = 2\,({\widehat u_T} - {\widehat u_S})\] Der Modulationsgrad m errechnet sich daraus zu: \[\begin{array}{l} m = \frac{{a - b}}{{a + b}}\; \Rightarrow \;\;m = \frac{{2\,({{\widehat u}_T} + {{\widehat u}_S}) - 2\,({{\widehat u}_T} - {{\widehat u}_S})}}{{2\,({{\widehat u}_T} + {{\widehat u}_S}) - 2\,({{\widehat u}_T} - {{\widehat u}_S})}}\\ m = \frac{{{{\widehat u}_S}}}{{{{\widehat u}_T}}} \end{array}\]

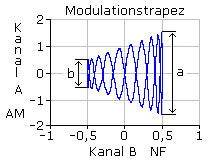
Im Sendebetrieb wird die Güte des Modulationssignals mit dem Modulationstrapez kontrolliert. Das Oszilloskop wird dazu in den A/B-Betrieb geschaltet, am Kanal A wird das AM-Signal und am Kanal B das NF-Informationssignal angeschlossen. Auch hier kann aus beiden vertikalen Auslenkungen links und rechts mithilfe der oben hergeleiteten Gleichung der Modulationsgrad errechnet werden.

Modulationsgrad und Bandbreite der AM

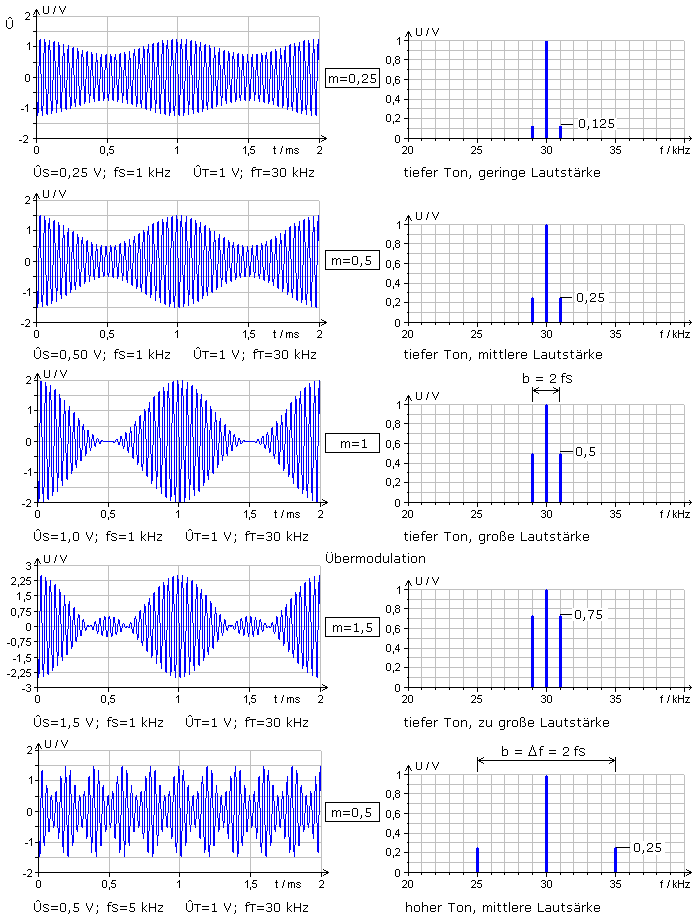
Der Modulationsgrad m der AM ist definiert als das Amplitudenverhältnis des Modulationssignals zum Trägersignal. Die Lautstärke eines Audiosignals wird von der NF-Signalamplitude bestimmt. Ein leises Signal beeinflusst die Trägeramplitude wenig, während ein lautes Signal zur großen Amplitudenänderung führt. Beim Modulationsgrad m = 1 sind Träger- und Modulationsamplitude gleich groß, wobei periodisch die Amplitude des AM-Signals null wird. Für die Praxis ist diese vollständige Modulation ungeeignet, da die Demodulatoren im Bereich der Nullstellen nicht korrekt arbeiten und das NF-Signal nicht unverzerrt zurück erhalten wird.

Ist die NF-Signalamplitude größer als die des Trägers, so wird m > 1. Dieser Zustand erzeugt eine Übermodulation und ein verzerrtes Modulationsprodukt. Eine Demodulation kann daraus kein unverzerrtes Originalsignal gewinnen. Die folgenden Diagramme zeigen zum Vergleich Zeit- und Frequenzdiagramme für unterschiedliche Modulationsgrade und Signalfrequenzen. Der Modulationsgrad kann mithilfe eines Spektrumanalysators oder der Fourieranalyse eines Softwaresimulationsprogramms ermittelt werden. bei der Eintonmodulation ist dazu das Verhältnis der Summe beider Amplituden der Seitenbänder zur Trägeramplitude zu bestimmen.

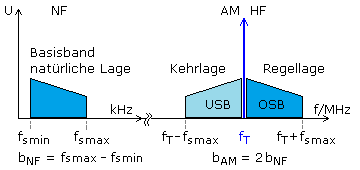
Bandbreite der AM

Die Bandbreite eines NF-Signals bestimmt die Bandbreite des modulierten AM-Signals. Sie ist doppelt so groß, da der HF-Träger symmetrisch von den beiden Seitenbändern eingeschlossen ist. Die Bandbreite des Modulators muss mindestens doppelt so groß sein wie die höchste zu übertragene Signalfrequenz. Die Bandbreite kommerzieller AM-Sender im Mittelwellenband ist international auf 9 kHz festgelegt. Benachbarte AM-Sender müssen diesen Trägerabstand einhalten. Nur unter diesen Voraussetzungen überschneiden sich die Seitenbänder benachbarter Sender nicht und die darin enthaltenen Informationen lassen sich unverfälscht zurückgewinnen. Im Rundfunksendebereich ist für die analoge AM die höchste übertragbare NF-Frequenz auf etwas weniger als 4,5 kHz begrenzt und ist etwas größer als die Bandbreite im analogen Telefonfestnetz. Das dort übertragene Sprachfrequenzband reichte von 300 Hz bis 3,4 kHz. Für höherwertige Musiksendungen ist diese Methode nicht geeignet.

Zur besseren Anschaulichkeit und Verständnis wurde die Amplitudenmodulation bisher nur mit einer einzelnen Modulationsfrequenz gezeigt. Sprache und Musik umfassen ein ganzes Frequenzspektrum im Basisband. Dieses Spektrum erscheint dann im AM-Signal in den Seitenbändern. Das rechts vom Träger liegende obere Seitenband OSB (im engl. Sprachraum USB = Upper Side Band) befindet sich in der Regellage. Die Frequenzabfolge entspricht der des Basisbands das um die Trägerfrequenz höher ist. Das untere Seitenband USB (im engl. Sprachraum LSB Lower Side Band) links vom Träger hat im Vergleich zum Basisband eine Kehrlage. In beiden Bändern liegen die modulierten tieferen Signalfrequenzen näher zum Träger als die höheren. Die Rückgewinnung der NF-Information erfolgt durch Demodulatoren. Für entsprechende Beispiele und deren Beschreibungen gibt es mit dem Titel Demodulation von AM-Signalen im Webprojekt eine eigene Seite.

Leistungsbilanz der AM

Für alle AM-Signale, die den mitgesendeten HF-Träger enthalten, benötigt der Träger den größten Teil der Sendeenergie. Das ist nicht so effektiv, da der Träger nur ein Hilfssignal ist. Abgesehen von Wärmeverlusten im Sender verteilt sich die gesamte AM-Senderleistung auf die reine Trägerleistung PT und die Leistung PS für jedes einzelne Seitenband. Es gilt: \({P_{AM}} = {P_T} + 2\,{P_{S}}\). Die Gesamtleistung der AM-Modulation ist vom Modulationsgrad m abhängig. Wird in der oben hergeleiteten Zeitfunktion der AM-Spannung die Spitzenspannung des Seitenbands unter Berücksichtigung des Modulationsgrads durch die Spitzenspannung des Trägers ersetzt, dann folgt mit \({\widehat u_S} = m \cdot {\widehat u_T}\): \[{u_{AM}}(t) = \frac{{m\,{{\hat u}_T}}}{2}\cos (\Omega - \omega )\,t + {\hat u_T}{\mkern 1mu} \cos (\Omega \,t) + \frac{{m\,{{\hat u}_T}}}{2}\cos (\Omega + \omega )\,t\] Für die Leistung am Widerstand gilt allgemein: \[P = \frac{{u_{eff}^2}}{R}\quad mit\quad {u_{eff}} = \frac{{\widehat u}}{{\sqrt 2 }}\quad \Rightarrow \quad P = \frac{{{{\widehat u}^2}}}{{2\,R}}\] Für die Träger- und Seitenbandleistungen am selben Widerstand gelten für den Träger PT und für das einzelne Seitenband PS: \[{P_T} = \frac{{\hat u_T^2}}{{2\,R}}\quad \quad {P_S} = \frac{{{{\left( {\frac{{m\,{{\hat u}_T}}}{2}} \right)}^2}}}{{2\,R}} = \frac{{{m^2}\,\hat u_T^2}}{{8\,R}}\] Angewendet auf die Zeitfunktion zur AM-Modulation folgt für die Gesamtleistung des AM-Signals: \[\begin{array}{l} {P_{AM}} = \frac{{\hat u_T^2}}{{2\,R}} + 2 \cdot \left( {\frac{{{m^2}\,\hat u_T^2}}{{8\,R}}} \right) = \frac{{\hat u_T^2}}{{2\,R}}\left( {1 + \frac{{{m^2}}}{2}} \right)\\ {P_{AM}} = {P_T}\left( {1 + \frac{{{m^2}}}{2}} \right) \end{array}\]

Die Leistung, die ein AM-Sender beim theoretisch maximalen Modulationsgrad m = 1 abstrahlt, verteilt sich zu 2/3 auf den Träger und zu 1/3 auf beide Seitenbänder. Das einzelne Seitenband nutzt zur Informationsübertragung nur 1/6 der gesamten Sendeenergie. Da zur verzerrungsfreien Demodulation des AM-Signals der Modulationsgrad m < 1 sein muss, ist das praktisch nutzbare Leistungsverhältnis deutlich schlechter.

Der Wirkungsgrad (eta) für die geträgerte ZSB-AM errechnet sich zu: \[\begin{array}{l} \eta = \frac{{{P_S}}}{{{P_{AM}}}} = \frac{{{P_S}}}{{{P_T} + 2\,{P_2}}}\\ \eta = \frac{{{m^2}\,\hat u_T^2}}{{4\,\hat u_T^2 + 2\,({m^2}\,\hat u_T^2)}}\\ \eta = \frac{{{m^2}}}{{4 + 2\,{m^2}}} \end{array}\]

Amplitudenmodulation am Modell der rotierenden Zeiger

Es wurde gezeigt, dass bei der Einton-Modulation einer hochfrequenten HF-Trägeramplitude mit einem NF-Informationssignal das Frequenzspektrum nach Fourier drei Frequenzlinien enthält. Im AM-Spektrum sind der HF-Träger und symmetrisch dazu im Abstand der NF-Frequenz zwei Seitenlinien zu erkennen. Die NF-Spektrallinie tritt nicht mehr auf. Das gleiche AM-Signal kann folglich durch eine lineare Überlagerung, einer Signaladdition dieser drei Frequenzen nach dem Verfahren der Fouriersynthese erzeugt werden. Der folgende Videoclip stellt in kurzen aufeinanderfolgenden Abschnitten diesen Vorgang dar. Die einzelnen Sequenzen sind mit erklärenden Texten versehen und das Video kann mithilfe der einblendbaren Controlleiste gesteuert werden.

In der Literatur und wissenschaftlichen Veröffentlichungen wird im Rotationsmodell an der Trägerspitze der OSB- und USB-Zeiger gegenläufig dargestellt. Die Kreisfrequenzen beider Zeiger werden durch +ωt und −ωt angegeben. Der Vorzeichenwechsel und die Änderung des Drehsinns entstehen durch den relativen Bezug auf den dazu mittig stehenden Träger.

Ausblick

Im Funkverkehr haben AM-Signale eine sehr große Reichweite. Im Lang- und Mittelwellenbereich verlaufen sie als sogenannte Bodenwellen und passen sich der Krümmung der Erdoberfläche gut an. Im Kurzwellenbereich kann die Raumwelle zwischen der Erde und den höher liegenden atmosphärischen Schichten mehrfach reflektiert werden. Die Reichweite selbst schwacher Kurzwellensender kann somit den ganzen Erdball umfassen.

Die schlechte Leistungsbilanz ist ein bedeutender Nachteil der Amplitudenmodulation. Mit speziellen Varianten wie der Einseitenbandtechnik oder einer AM mit unterdrücktem Träger gibt es Verbesserungen, die nur mit einem größeren technischen Aufwand im Sender- und Empfängerbereich erreicht werden.

Elektrische Störungen beeinflussen oftmals die Amplitude und werden bei der Modulation mit erfasst. Störungen während der Übertragung des AM-Signals, beispielsweise Einstreuungen in ein Kabelnetz, Sende- und Empfangsschwankungen bei Funkstrecken, machen sich ebenfalls als Amplitudenänderungen bemerkbar. Bei der Signalrückgewinnung durch Demodulation können diese kurzzeitigen Amplitudenstörungen nicht ausgefiltert werden und verschlechtern die Empfangsqualität.