Parameterfunktion, Funktionsschar und Ortskurve

Viele physikalische Experimente, die von bestimmten Parametern abhängen, lassen sich mathematisch durch allgemeingültige Funktionsgleichungen beschreiben. Ein sehr einfaches Experiment ist die Bestimmung der Abhängigkeit von Strom und Spannung an einem Widerstand. Die variable Größe ist die angelegte Spannung und der Funktionswert der gemessene Strom. Gesucht ist der funktionelle Zusammenhang des Stroms I von der angelegten variablen Spannung U, also I = f(U). Der Parameter ist ein frei wählbarer Widerstand. Wird der Versuch mit Wechselspannung und einer Spule oder einem Kondensator als Wechselstromwiderstand durchgeführt, kommt die Frequenz als zusätzlicher Parameter hinzu. Für jede Messreihe bleiben die Parameter konstant. Werden sie verändert, entstehen neue Messreihen. Beeinflussen mehrere Parameter die Messungen, so sollte zur Bestimmung der allgemeingültigen Funktionsgleichung in jeder Messreihe immer nur ein Versuchsparameter variiert werden.

In der allgemeinen Funktionsgleichung y = f(x) = m·x + n oder geschrieben als y = f(x) = a·x + b ist x die Variable und y die davon abhängige Größe. Der Faktor vor x und das absolute Glied sind noch frei wählbare Funktionsparameter. Zu Darstellung des Funktionsgraphen im rechtwinkligen Achsenkreuz wird für jede Wertetabelle, vergleichbar mit einer Messreihe, jedem Parameter ein definierter unveränderlicher Wert zugewiesen. Das daraus folgende Funktionsbild ist eine Gerade, die für andere Parameterwerte einen anderen Verlauf hat. Werden in das gleiche Achsensystem mehrere Funktionsbilder in Abhängigkeit unterschiedlicher Parameter eingetragen, entsteht eine Funktionsschar. Die beiden Beispiele zeigen Funktionsscharen für Geraden mit m als variablem Steigungsparameter oder n als variablem Achsenabschnittsparameter. In der zugehörigen allgemeinen Parameterfunktion wird der Parameter als Index geschrieben.

In beiden Beispielen ist x die unabhängige Funktionsvariable, die in der Funktionsgleichung f(x) in der Klammer steht. Der variable Parameter wird als Index fm(x) oder fn(x) geschrieben und ist für jeden einzelnen Funktionsgraphen konstant. Die eigentliche Funktion ändert sich nicht und hat anstelle eines fixen Parameters einen allgemeinen Parameter. Wird er geändert, entsteht als gemeinsames Funktionsbild eine Funktionsschar.

Das Differenzieren und Integrieren bezieht sich immer auf die unabhängige Variable und nicht auf den Parameter. Die bekannten Regeln gelten unverändert, weil der Parameter von der Funktionsvariablen unabhängig ist und wie ein konstanter Zahlenwert behandelt wird. Die folgenden Beispiele sollen das verdeutlichen.

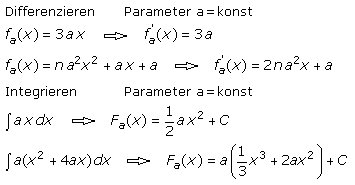
Parameterfunktionen berechnen

Im folgenden Beispiel soll die Parameterfunktion einer Parabel untersucht werden. Das lineare und das absolute Glied haben mit a den gleichen Parameter. Er beeinflusst die Lage des Scheitelpunkts und der möglicherweise vorhandenen Nullstellen der Parabel. Zur Berechnung der Nullstellen wird wie bisher der Funktionswert null gesetzt und anschließend die quadratische Gleichung gelöst. Der einzige Unterschied ist das Auftreten des noch frei bestimmbaren Parameters in den Lösungen. Die x-Werte für die Nullstellen sind folglich Funktionen des Parameters.

Die Funktion hat nur dann reelle Nullstellen, wenn der Ausdruck unter der Wurzel, die Diskriminante nicht negativ ist. Der Parameterwert a = 0 führt zur Normalparabel mit der gemeinsamen Null- und Scheitelstelle im Koordinatenursprung. Mit a > −4 wird die Diskriminante auch null, sodass es eine weitere gemeinsame Null- und Scheitelstelle geben wird. Die Koordinaten der Nullpunkte werden durch Einsetzen der x-Koordinaten in die Parameterfunktion errechnet. Bei a = −4 liegt der der gemeinsame Null- und Scheitelpunkt P(2/0).

Zur Bestimmung der Extremstellen ist die 1. und 2. Ableitung wie gewohnt nur nach der Variablen x zu bilden. Der von x unabhängige Parameter wird wie eine Konstante behandelt. Die 2. Ableitung charakterisiert die Extremstelle als Hochpunkt oder Tiefpunkt. Die y-Koordinate der Extremstelle errechnet sich durch Einsetzen der x-Koordinate in die Parabelfunktion. Die Lage ist vom Parameter a abhängig und fällt wie zu erwarten für a = 0 und a = −4 mit den dort bestimmten Nullstelle N1(0/0) und N2(2/0) zusammen.

Die 2. Ableitung ist vom Parameter unabhängig und in diesem Beispiel größer null. Für alle Parameterwerte ist der Extremalpunkt somit immer ein Tiefpunkt.

Ortskurve

Auf der Ortskurve oder Ortslinie liegen alle Punkte mit einer für die Parameterfunktion bestimmten Eigenschaft wie beispielsweise Extrempukte, Wendepunkte und Sattelpunkte. In den meisten Fällen kann für die Ortskurve eine Funktionsgleichung bestimmt werden. Eine besondere Ortskurve ist die Parallele zur y-Achse, die nicht der Definition einer Funktion entspricht und daher eher als Ortslinie bezeichnet wird. Mit den zuvor bestimmten Koordinaten eines charakteristischen Kurvenpunkts der Parameterfunktion werden für die x- und y-Koordinate zwei Bestimmungsgleichungen aufgestellt, aus denen die Ortskurve hergeleitet wird.

Sind für eine Parameterfunktion die Koordinaten des charakteristischen Punkts nicht vom Parameter abhängig, gibt es keine Ortskurve oder Ortslinie. Ist der Parameter nur in der y-Koordinate vorhanden, dann ist die Ortslinie eine Parallele zur y-Achse, da die x-Koordinate für alle Parameterwerte konstant bleibt. Ist der Parameter nur in der x-Koordinate vorhanden, dann verläuft die Ortslinie/Ortskurve parallel zur horizontalen x-Achse. Tritt der Parameter in der x- und y-Koordinate auf, dann existiert eine Ortskurve.

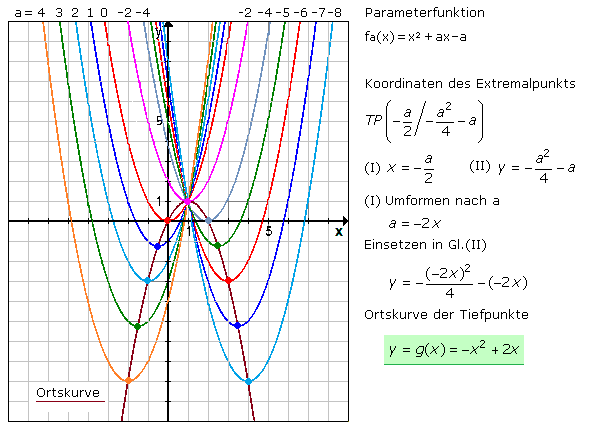
Für die gegebene Parameterfunktion folgt die Herleitung der Ortskurve für die Tiefpunkte. Das Ergebnis ist eine Parabel. Die Grafik zeigt den Verlauf der Ortskurve und für einige Parameter die Funktionsschar. Die Tiefpunkte sind hervorgehoben und liegen alle auf der Ortskurve.

Gemeinsame Punkte einer Kurvenschar

Bei der untersuchten Parameterfunktion erkennt man mindestens einen gemeinsamen Punkt. Zur Berechnung werden zwei Funktionsgleichungen aufgestellt, die anstelle des Parameters a zwei unterschiedliche 'Ersatzparameter' haben. Gibt es gemeinsame Punkte, dann erfüllen die Punktkoordinaten beide Funktionsgleichungen, die zur Berechnung gleich gesetzt werden. Es wird die Variable x berechnet und durch Einsetzen des Werts in die Parameterfunktion folgt der y-Wert. Der gemeinsame Punkt P(1/1) ist in der Grafik oben ablesbar.