Operatoren der Widerstände und Leitwerte
Im Gleichstromkreis wird am Ohmschen Widerstand elektrische Leistung in eine andere Wirkleistung wie beispielsweise Licht, Wärme oder Bewegung umgesetzt. Der Ohmsche Widerstand wird auch als Wirkwiderstand bezeichnet. Im Wechselstromkreis kommen mit dem Kondensator und der Spule zwei weitere Widerstandsarten mit neuen Eigenschaften hinzu. Der Gesamtwiderstand einer Wechselstromschaltung wird als Wechselstromwiderstand oder Impedanz bezeichnet. Sie hat das Formelzeichen Z mit der Einheit Ω, Ohm und ist das Amplitudenverhältnis aus der anliegenden Spannung und der daraus resultierenden Stromstärke. Die Impedanz einer Schaltung ist von der Frequenz abhängig und somit bei konstanter Eingangsspannung keine konstante Größe. Die komplexe mathematische Darstellung sinusförmiger zeitabhängiger Spannungen und Ströme führt zu den folgenden Gleichungen.
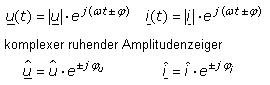
Die Berechnung der Impedanz einer Schaltung mit Spannungs- und Stromwerten ist nur bei einer konstanten Frequenz sinnvoll. Alle Betrachtungen lassen sich vereinfacht für ruhende Amplitudenzeiger durchzuführen. Die komplexen Größen können dabei unterschiedliche Nullphasenwinkel haben. Die Impedanz ist ebenfalls eine komplexe Größe mit einem Realteil und einem Imaginärteil. Die Wechselstromwiderstände der drei Bauteile R, L und C werden als Widerstandsoperatoren bezeichnet. Sie haben in der komplexen Zahlenebene eine unveränderbare definierte Richtung. Ihr Anfangspunkt liegt standardmäßig im Koordinatenursprung, können aber durch Parallelverschiebung in der Lage verändert werden. In der zeichnerischen Darstellung werden die Operatoren als Strecken dargestellt, während die Zeiger durch eine Pfeilspitze gekennzeichnet sind.
Operator des Wirkwiderstands
Das besondere Kennzeichen des Widerstandsoperators ist die fehlende Phasenverschiebung zwischen Strom und Spannung. Der Operator liegt in Richtung der Achse positiver reeller Einheiten.
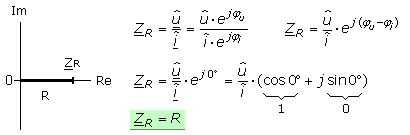
Operator des Wirkleitwerts
Der Kehrwert des Widerstandsoperators ist der Operator des Wirkleitwerts. Die bekannten Beziehungen zwischen Widerstand und Leitwert haben auch in der komplexen Rechnung weiterhin Bestand.
Operator des induktiven Blindwiderstands
Das besondere Kennzeichen einer Induktivität ist die Phasenverschiebung bei der die Spannung um 90° dem Strom vorauseilt. Der Operator liegt daher in Richtung der Achse positiver imaginärer Einheiten.
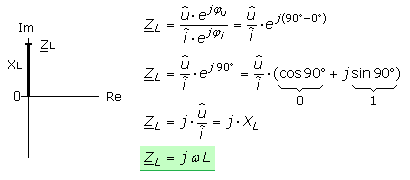
Operator des induktiven Blindleitwerts
Der Leitwertoperator errechnet sich als Kehrwert zum Operator des induktiven Blindwiderstands. Der Phasenwinkel ist unverändert und die Spannung eilt dem Strom um 90° voraus. Ein komplexer Nenner wird reell, wenn man den Bruch mit seinem konjugiert komplexen Nenner erweitert.
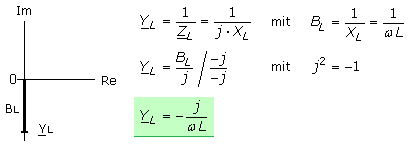
Operator des kapazitiven Blindwiderstands
Das besondere Kennzeichen der Kapazität ist die Phasenverschiebung, wo der Strom um 90° der Spannung vorauseilt. Der Operator liegt daher in Richtung der Achse negativer imaginärer Einheiten.
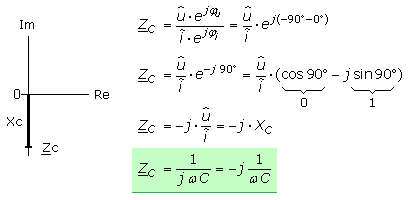
Operator des kapazitiven Blindleitwerts
Der Leitwertoperator ist der Kehrwert des Operators des kapazitiven Blindwiderstands. Der Phasenwinkel bleibt unverändert, wobei der Strom um 90° der Spannung vorauseilt. Der Operator liegt auf der positiven Achse der imaginären Einheiten.
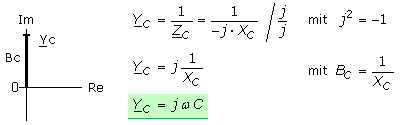
Operator des Scheinwiderstands
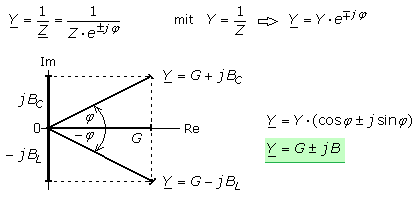
Der Scheinwiderstand, auch Impedanz oder Wechselstromwiderstand, ist ein zusammengesetzter Widerstand mit reellem Wirkanteil und imaginären Blindanteilen. Mathematisch definiert ist es der Quotient aus anliegender Wechselspannung und dem sich einstellenden Wechselstrom, wobei die Effektivwerte oder die Spitzenwerte eingesetzt werden können. Zwischen Strom und Spannung besteht ein Phasenwinkel, der Werte zwischen ±90° aufweisen kann.
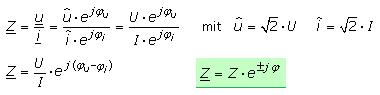
Die Zerlegung des Operators in seine Wirk- und Blindanteile geschieht durch Umwandlung der Exponentialform in die Normalform.
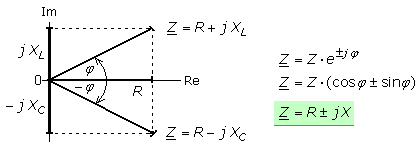
Operator des Scheinleitwerts
Bildet man den Kehrwert des oben hergeleiteten Scheinwiderstands, so kommt es im Exponenten zum Vorzeichenwechsel. Die Zerlegung des Operators des Scheinleitwerts in seine Komponentenschreibweise erfolgt ebenfalls über die trigonometrische Form.