Lineare Gleichungssysteme
In einer linearen Gleichung 1. Grades liegt die unbekannte Größe in der 1. Potenz vor. Ist der Koeffizient der Unbekannten ungleich null, kann man die Gleichung so umschreiben, dass die Unbekannte frei auf der einen Seite des Gleichheitszeichens steht. Man erhält die allgemeine Lösungsgleichung.
Normalform: a1·x1 + a0 = 0 daraus folgt: x1 = −a0 / a1 mit a1 ≠ 0
Ein lineares Gleichungssystem besteht aus mehreren linearen Gleichungen und Unbekannten in der 1. Potenz, die in den Gleichungen vorkommen und zusammen gültig sind. Zum Berechnen werden mindestens so viele Gleichungen benötigt, wie es Unbekannte gibt. Mithilfe von Einsetzungs-, Gleichsetzungs- und Additionsverfahren lassen sich nacheinander die einzelnen Unbekannten bestimmen. Programmierbare Verfahren, wo Gleichungen manuell nicht umgestellt werden können, verwenden Determinanten zur Bestimmung der Unbekannten.
Eliminierungsverfahren nach Gauß
Auf ein lineares Gleichungssystem werden Additions- und Multiplikationsverfahren angewendet. Dabei entstehen äquivalente Umformungen der gegebenen Gleichungen, wobei die Lösungsmenge des linearen Gleichungssystems erhalten bleibt. Das Ziel ist es, nacheinander aus jeder Gleichung eine der Unbekannten zu eliminieren, sodass am Ende eine Bestimmungsgleichung für die letzte Unbekannte bleibt. Die folgenden Regeln gelten für den Gauß-Algorithmus:
- Gleichungen können miteinander vertauscht werden.
- Jede Gleichung kann mit einem reellen Faktor ungleich null multipliziert werden.
- Zu jeder Gleichung kann das Vielfache einer anderen Gleichung addiert werden.
Das folgende konkrete Beispiel zeigt den Ablauf des Gauß-Algorithmus für ein lineares Gleichungssystem mit den Gleichungen I, II und III und drei Unbekannten. Die Unbekannte x1 mit dem niedrigsten Koeffizienten steht in der Gl.(I) an der richtigen Stelle und bleibt im weiteren Verlauf unverändert als Eliminationszeile Gl.(E) bestehen.
In den Gl.(II) und (III) ist x1 zu eliminieren. Die Gl.(E) ist mit einem Faktor zu multiplizieren, sodass bei der Addition mit Gl.(II) in der neuen Gl.(II') und Gl.(III') die erste Unbekannte wegfällt. Jetzt wird die Gl.(II') zur nächsten Eliminationszeile E2 und bleibt unverändert.
In der Gl.(III') ist die Unbekannte x2 zu eliminieren. Das wird erreicht, wenn die Gl.(II') mit dem Faktor (−1) multipliziert und zur Gl.(III') addiert wird. In der neuen Gl.(III'') steht nur noch die dritte Unbekannte und kann direkt berechnet werden. Die Division durch den Koeffizienten 3 führt zum ersten Ergebnis in der Eliminationszeile E3.
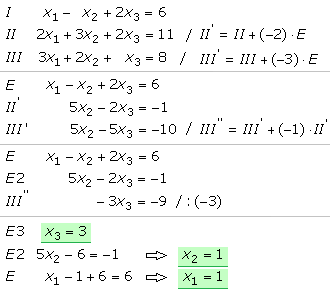
Wird das Ergebnis der Zeile E3 in die Zeile E2 eingesetzt, kann die nächste Variable errechnet werden und mit dem Einsetzen der Ergebnisse in die Zeile E folgt der Wert für die letzte Variable. Beim Gauß-Algorithmus kommt es nicht auf die Reihenfolge an, nach der die Unbekannten eliminiert werden.
Gauß-Algorithmus in Stufenform
Das lineare Gleichungssystem wird so sortiert, dass alle Variablen in gleicher Reihenfolge und die Ergebnisse als absolute Glieder getrennt auf der anderen Seite des Gleichheitszeichens stehen. Das kann auch übersichtlich in einer Art Tabelle als Matrix geschrieben werden. Man erhält links für die Koeffizienten eine quadratische Matrix. Das Ziel ist es, dass unterhalb ihrer Diagonalen in einer Ecke die Koeffizienten alle den Wert null haben.
Vor dem Bilden der Stufenform dürfen innerhalb der Tabelle die Zeilen vertauscht werden. Sie dürfen mit einer Zahl multipliziert oder durch eine Zahl dividiert werden. Die Zeilen dürfen untereinander addiert oder subtrahiert werden.
Das Verfahren soll auf das oben berechnete Gleichungssystem angewendet werden. Die Wahl der Ecke ist egal, hier soll es die linke Ecke unterhalb der Hauptdiagonalen sein. Die erste Zeile bleibt unverändert. Wird sie mit dem Faktor (−2) multipliziert und zur zweiten Zeile addiert, dann beginnt die zweite Zeile mit null. Wird die erste Zeile mit (−3) multipliziert und zur dritten Zeile addiert, dann ist der erste Wert dieser Zeile ebenfalls null.
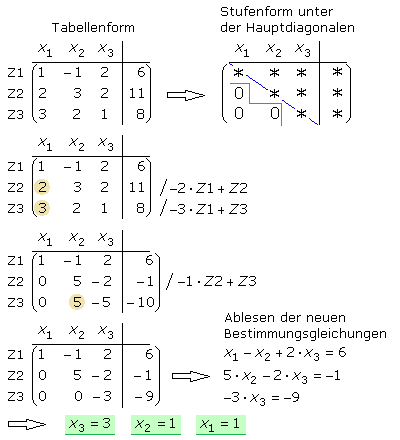
Der Wert der zweiten Spalte in der dritten Zeile muss zu null werden. Damit die erste Null in der zweiten Zeile bestehen bleibt, kann jetzt nur noch mit den Zeilen 2 und 3 gearbeitet werden. Die zweite Zeile wird mit (−1) multipliziert und zur dritten Zeile addiert. In der Zeile 3 kann die Variable x3 direkt berechnet werden. Ihr Wert wird in die Bestimmungsgleichung der Zeile 2 eingesetzt, um die Variable x2 zu berechnen. Im letzten Schritt wird dann der Wert der Variablen x1 berechnet.
Gauß-Jordan-Algorithmus
Dieses Verfahren ist eine Erweiterung der Stufenform. Die Koeffizientenmatrix wird weiter zur Einheitsmatrix entwickelt. Bei ihr stehen auf der Hauptdiagonalen nur die Werte 1 und alle anderen Werte oberhalb und unterhalb sind null. In der erweiterten Koeffizientenmatrix, mit der rechts durch den vertikalen Strich abgetrennten Ergebnisspalte, kann dann der Wert jeder Variablen direkt abgelesen werden.
Die Rechenschritte entsprechen der Vorgehensweise für den Gauß-Algorithmus. In der ersten Zeile der Matrix steht der Koeffizient der ersten Variablen und muss ungleich null sein. Falls das nicht zutrifft, sind vor dem Beginn der Rechnungen einzelne Gleichungszeilen gegeneinander zu tauschen. Die erste Zeile bleibt unverändert. Die Folgezeilen werden mit ihr so verrechnet, dass alle Werte in der ersten Spalte ab der zweiten Zeile den Wert null erhalten. Die Vorgehensweise wird auf die markierte Untermatrix übertragen, deren erste Zeile, das ist die zweite Zeile der Koeffizientenmatrix unverändert bleibt. Ebenso werden die Nullen links der Hauptdiagonalen mithilfe der dritten Zeile erzeugt.

Im Gauß-Jordan-Algorithmus arbeitet man sich jetzt in umgekehrter Reihenfolge von der untersten zur ersten Zeile vor. Ist der letzte Wert in der Koeffizientenmatrix noch nicht 1, so muss die letzte Zeile der erweiterten Koeffizientenmatrix durch ihn dividiert werden. Die letzte Zeile bleibt dann unverändert. Mit ihr werden die darüber stehenden Zeilen so verrechnet, dass alle anderen Werte der vierten Spalte in der Koeffizientenmatrix den Wert null erhalten. Im weiteren Verlauf werden mit der dritten Zeile und danach mit der zweiten Zeile die notwendigen Nullen oberhalb der Hauptdiagonalen berechnet. Stehen auf der Hauptdiagonalen nur Einsen, dann lassen sich die gesuchten Variablenwerte Zeile für Zeile aus der letzten Spalte direkt ablesen.
Cramersche Regel
Lineare Gleichungssysteme lassen sich mithilfe von Determinanten lösen. Das Verfahren dazu wurde in der ersten Hälfte des 18. Jahrhunderts vom Schweizer Mathematiker Gabriel Cramer entwickelt. Man schreibt die Gleichungen in der Form, dass links vom Gleichheitszeichen die Variablen mit ihren Koeffizienten und rechts die Ergebnisse als absolute Glieder ohne Variablen stehen. Ein System aus n Gleichungen und n Unbekannten stellt ein quadratisches lineares (n, n)-Gleichungssystem dar. Mit den daraus folgenden quadratischen Determinanten lassen sich eindeutige Lösungen finden, wenn die Koeffizientendeterminante ungleich null und nicht alle absoluten Glieder in der Ergebnisspalte null sind.
Die einzelnen Gleichungen werden so sortiert, dass die Variablen in gleicher Reihenfolge stehen. Als Erstes erstellt man die Determinante mit den Koeffizienten der Variablen. Zur Berechnung der einzelnen Variablen ersetzt man in dieser Koeffizientendeterminante nacheinander die Spalten durch die Ergebnisspalte und stellt die zugehörigen Hilfsdeterminanten auf. Man ermittelt die Werte aller Determinanten. Den gesuchten Zahlenwert der Variablen erhält man, indem der Wert einer Hilfsdeterminante durch den Wert der Koeffizientendeterminante geteilt wird.
Das eingangs berechnete lineare (3, 3)-Gleichungssystem soll hier mithilfe von Determinanten gelöst werden. Nach dem Erstellen der Koeffizientendeterminante werden nacheinander die Hilfsdeterminanten durch den Ersatz der jeweiligen Spalte mit der Ergebnisspalte gebildet. Die Werte der Determinanten können mithilfe der Regel nach Sarrus ermittelt werden.

Die Ergebnisse beider Verfahren sind identisch. Das Verfahren nach Cramer ist für die in der Praxis oft vorkommenden nicht allzu großen Gleichungssysteme manuell gut durchführbar. Es kann programmiert werden, dann lassen sich auch umfangreiche Gleichungssysteme automatisch berechnen.