Funktion und Umkehrfunktion
Definitionsmenge, Wertemenge, Bildmenge
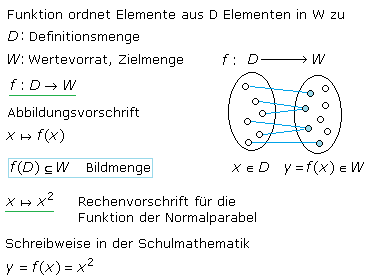
In der Mathematik sind Funktionen und Abbildungen identische Bezeichnungen, vielleicht mit der Spezifizierung, dass der Funktionsbegriff mehr auf die Verarbeitung numerischer Werte bezogen ist. Eine Funktion f weist jedem Element einer bestimmten Menge, der Definitionsmenge (Definitionsbereich) eindeutig nur ein Element einer Zielmenge (Wertevorrat) zu. Im ebenen kartesischen Koordinatensystem sind die Elemente der Definitionsmenge auf der horizontalen Achse und die Elemente der Zielmenge, des Wertevorrats auf der vertikalen Achse angeordnet. In der Schulmathematik ist in vielen Fällen die horizontale Achse die x-Achse und die vertikale Achse die y-Achse. Die Funktion wird als y = f(x) oder als allgemeine Abbildungsvorschrift x ↦ f(x) geschrieben. Für f(x) muss noch die gewünschte Rechenanweisung angegeben werden. Für eine lineare Funktion beispielsweise f(x) = 3·x + 2 und für eine Sinusfunktion f(x) = sin(x). Wichtig ist, dass auf jedes Element der Definitionsmenge die Rechenvorschrift der Funktion y = f(x) angewendet wird, um es genau einem Element der Zielmenge zuzuordnen.
In vielen Skripten und Büchern steht für die Zielmenge der Buchstabe W und wird oft Wertemenge genannt. Optimaler wäre Wertebereich/Wertevorrat und die Elemente der Funktionswerte f(x) werden als Bildmenge bezeichnet. Es kommt leicht zu Mehrdeutigkeiten oder Missverständnissen, wenn nicht eindeutig erkannt werden kann, ob die Funktionswerte f(x) die gesamte Wertemenge und damit die Bildmenge ist, oder ob nur die Teilmenge des Wertebereichs, einer größeren Ziel-/Wertemenge gemeint ist.
Eine Funktion bildet alle Elemente einer Menge, der Definitionsmenge (D) auf Elemente einer Zielmenge (W), dem Wertevorrat ab. Alle Elemente in W, die aus der Zuordnung x ↦ f(x) entstehen, gehören zur Bildmenge f(D). Sie ist mindestens eine Teilmenge der Zielmenge W.
Im Koordinatensystem dargestellt ergeben alle Funktionswerte als Elemente der Bildmenge den Funktionsgraphen. Im Folgenden soll die Funktion eine reelle Zahlenmenge auf eine andere reelle Zahlenmenge abbilden. Mit der Rechenvorschrift x ↦ x² werden in der Zielmenge nur positive Elemente getroffen und die Bildmenge ist eine Teilmenge der Zielmenge. Mit den Rechenvorschriften x ↦ 2·x oder x ↦ x³ wird jedem Element der Definitionsmenge ein bestimmtes Element der Zielmenge zugeordnet. Die Bildmenge ist gleich der Zielmenge, wo alle Elemente der reellen Zahlen eine Zuordnung erhalten. Sind die Funktionswerte f(x) größer null, dann verläuft der Funktionsgraph oberhalb der horizontalen x-Achse. Mit f(x) < 0, liegt das Funktionsbild unterhalb der x-Achse. Wo die x-Achse geschnitten oder berührt wird, befindet sich eine Nullstelle.
Monotonie
Wird der Funktionswert f(x) in Richtung größerer x-Werte größer oder bleibt gleich, dann wird die Funktion als monoton wachsend bezeichnet. Mit x1 < x2 folgt f(x1) ≤ f(x2). Streng monoton wachsend oder steigend verhält sich eine Funktion, wenn ihr Funktionswert in Richtung größerer x-Werte immer größer als zuvor ist. Mit x1 < x2 folgt f(x1) < f(x2). Bei der umgekehrten Eigenschaft einer monoton fallenden oder abnehmenden Funktion ist der Funktionswert mit abnehmendem x-Wert kleiner oder gleich dem vorherigen Wert. Bei einer streng monoton fallenden Funktion ist der Funktionswert in Richtung kleinerer x-Werte immer kleiner als zuvor.
Injektivität
Der Funktionsterm bestimmt die Zuordnung der Elemente aus der Definitionsmenge D auf die Elemente der Zielmenge W. Die Bildmenge muss mindestens eine Teilmenge der Zielmenge sein. Die Funktion ist injektiv, wenn es für die Elemente der Bildmenge höchstens ein Element in der Definitionsmenge gibt. Verschiedene Elemente der Definitionsmenge ergeben verschiedene Werte der Bildmenge.
Injektivität: Jedes Element der Definitionsmenge weist auf genau ein Element der Bildmenge. Zu jedem y = f(x) gibt es höchstens einen x-Wert. Mit x1 ≠ x2 folgt f(x1) ≠ f(x2).
Die folgende Skizze zeigt, dass die Injektivität für streng monoton steigende oder fallende Funktionen erfüllt ist. Im einfachsten Fall sind das allgemeine lineare Funktionen wie y = f(x) = m·x + n. Auch Funktionen wie y = f(x) = x³ und y = f(x) = 1 / x sind injektiv. Für die Normalparabel gilt es nur dann, wenn die Definitionsmenge auf nur einen Parabelast eingeschränkt ist.
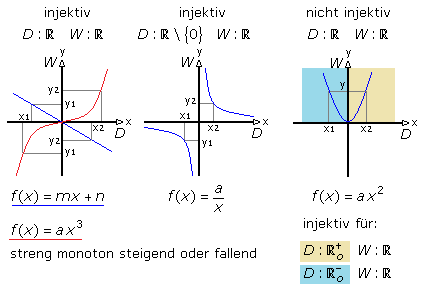
In der Skizze links gehören die Elemente der Definitions- und Zielmenge zu den reellen Zahlen. Für die Hyperbelfunktion sind in der Definitionsmenge alle reellen Zahlen außer der Null erlaubt. Die dargestellten Funktionen sind injektiv. Rechts in der Skizze erfolgt die Zuordnung von reell nach reell. Die Parabelfunktion hat für jeden Funktionswert ungleich null zwei Elemente in der Definitionsmenge. Die gesamte Parabelfunktion ist nicht induktiv. Sie wird nur dann induktiv, wenn die Definitionsmenge auf nur positive oder negative Werte einschließlich der Null begrenzt wird. Ist die Zielmenge weiterhin für alle reellen Zahlen definiert, dann ist die Bildmenge des jeweiligen Parabelastes eine Teilmenge davon. In ihr gibt es für jedes Element nur ein Element aus der Definitionsmenge und die Induktivität ist erfüllt.
Surjektivität
Die Rechenvorschrift ordnet jedem Element der Definitionsmenge ein Element der Zielmenge zu. Gleiche Elemente der Bildmenge dürfen auch mehrfache Zuordnungen von verschiedenen Elementen der Definitionsmenge haben. Die Bildmenge muss gleich der Zielmenge und keine Teilmenge davon sein. Von der Bildmenge her gesehen bedeutet Surjektivität, dass jedes Element mindestens einmal mit einem Element der Definitionsmenge verbunden ist.
Surjektivität: Alle Elemente der Zielmenge W bilden die Bildmenge und jedes Element der Zielmenge hat eine Zuordnung. Mit y = f(x) und y ∈ W folgt ∃ x ∈ D. Es existiert mindestens ein Element x in D.
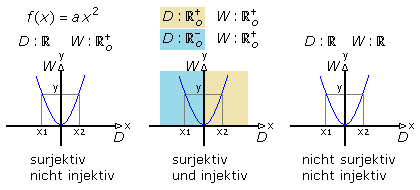
Links im Bild ist die Zielmenge auf positive reelle Werte einschließlich der Null begrenzt. Jedes Element der Definitionsmenge wird mindestens einmal auf ein Element der Zielmenge abgebildet. Da die Rechenvorschrift nur positive Funktionswerte bildet, ist die Zielmenge gleich der Bildmenge. Die Funktion ist surjektiv. Sie ist nicht injektiv, denn außer für x ≠ 0 hat jeder Funktionswert f(x) zwei Elemente in der Definitionsmenge. In der Bildmitte sind Definitions- und Zielmenge so definiert, dass die Rechenvorschrift nur zur Abbildung eines Parabelastes führt. Die Funktion ist wie zuvor surjektiv und zusätzlich injektiv. Rechts im Bild sind beide Mengen uneingeschränkt reell. Die Funktion ist nicht injektiv, denn es gibt Mehrfachabbildungen von D auf W. Sie ist auch nicht surjektiv, denn die Bildmenge ist eine Teilmenge der Zielmenge W. Negative reelle Zahlen erhalten keine Zuordnung.
Am Funktionsgraph kann die Surjektivität nicht so einfach abgelesen werden wie die Injektivität. Eine Exponentialfunktion x ↦ exp(x), die Elemente der reellen Definitionsmenge auf das Zielintervall der positiven reellen Zahlen einschließlich der Null abbildet, ist injektiv aber nicht surjektiv. Der Funktionsgraph nähert sich dem Wert f(x) = 0 nur asymptotisch. Die Bildmenge bleibt Teilmenge der Zielmenge. Diese Funktion ist surjektiv, wenn die Zielmenge auf alle positiven Zahlen unter Ausschluss der Null begrenzt ist.
Bijektivität
Injektivität und Surjektivität schränken sich gegenseitig ein. Bei der Injektivität darf die Zielmenge größer als die Bildmenge sein. Jedes Element der Definitionsmenge darf auf nur genau einem Element der Zielmenge abgebildet sein. Das entspricht einer eins zu eins Zuordnung zwischen Definitions- und Bildmenge. Die Surjektivität erlaubt die mehrfache Zuordnung eines Elements der Definitionsmenge zum gleichen Element in der Bildmenge, die genau der Zielmenge entsprechen muss. Eine Funktion, die beide Eigenschaften erfüllt, ist bijektiv. Die Elemente der Definitionsmenge sind den Elementen der Zielmenge genau eins zu eins zugeordnet und die Zahl der Elemente beider Mengen ist gleich. Die Bildmenge ist gleich der Zielmenge. Mathematiker bezeichnet die Zuordnung als eineindeutig, das Kriterium für die Umkehrbarkeit einer Funktion. Von der Bildmenge kann eindeutig auf die Definitionsmenge geschlossen werden.
Bijektivität: Zu jedem Element der Definitionsmenge gibt es nur genau ein Element in der Zielmenge: Die Anzahl der Elemente in der Definitions- und Zielmenge, der Bildmenge ist gleich.
Umkehrfunktionen
Für einen schnellen Überblick zum Verlauf des Funktionsgraphen im Koordinatensystem ist eine Wertetabelle gut geeignet. Die Funktion bildet alle Elemente aus dem Definitionsbereich D auf die Elemente der Zielmenge W ab. Zu den Kriterien der Umkehrbarkeit gehört, dass bei der Abbildung jedes Element in der Bildmenge maximal einmal vorkommt. Damit ist die Injektivität erfüllt. Verschiedene Elemente aus D ergeben immer verschiedene Elemente in W. Die Zuordnung muss für jedes Element der Zielmenge mindestens einmal erfolgen. Damit wird die Zielmenge zur Bildmenge, die oft als Wertemenge f(D) bezeichnet wird und die Surjektivität ist erfüllt. Bei der Umkehrfunktion ist die Wertetabelle vertauscht und es wird eine Zuordnung gesucht, die alle Elemente der Bildmenge eindeutig der einstigen Definitionsmenge, der nunmehr neuen Bildmenge zuordnet. Mathematisch muss f(D) = W gelten, wobei die Bildmenge und die Definitionsmenge gleich viele Elemente haben. Der Mathematiker verlangt für die Umkehrbarkeit einer Funktion, dass sie sowohl injektiv als auch surjektiv, also bijektiv ist. In der Technik und im Ingenieurbereich reicht die Injektivität mit der eindeutigen eins zu eins Zuordnung der Elemente aus.
Gibt es zu einer Funktion f: D → W eine Funktion g: W → D, und gilt g(f(x)) = x für alle Elemente x ∈ D und weiterhin f(g(y)) = y für alle Elemente y ∈ W, dann ist g die Umkehrfunktion von f.
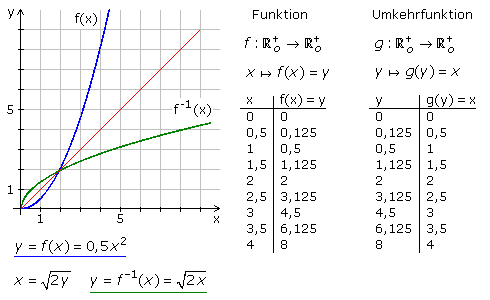
Im Koordinatensystem dargestellt ist die Umkehr- oder inverse Funktion der an der Winkelhalbierenden y = x gespiegelte Funktionsgraph. Wird eine bijektive Funktion nach ihrer Variablen aufgelöst, so führt das zur Umkehrfunktion. Sie macht die Rechenvorschrift der ursprünglichen Funktion rückgängig. Soll der Graph der Umkehrfunktion im selben Koordinatensystem wie die Ursprungsfunktion dargestellt werden, so kann vor oder nach der Umformung x mit y vertauscht werden.

Wurzelfunktion
Um für eine quadratische Funktion die Umkehrfunktion zu erstellen, muss der Definitions- und Zielbereich so weit eingeschränkt werden, dass jedes Element aus D zu genau einem Element in W führt. Die Anzahl der Elemente in W und im Bildbereich müssen gleich sein. Der Bildbereich f(D) ist dann auf einen streng monoton verlaufenden Parabelast begrenzt. Die Umkehrfunktion in der nicht komplexen Algebra ist die Wurzelfunktion mit nur positivem Radikand, dem Wert aus dem die Wurzel zu ziehen ist.
Logarithmusfunktion
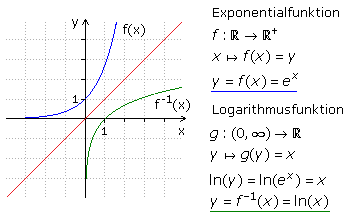
Die Umkehrung einer Exponentialfunktion führt zur Logarithmusfunktion. Für den Mathematiker muss auch hier die Definitions- und Bildmenge genau definiert sein, während dem technischen Ingenieur die Injektivität, oder das streng monotone Verhalten der Exponentialfunktion genügt. Die einfache e-Funktion bildet reelle Zahlen auf reelle Zahlen ab, ist aber nicht surjektiv, da in der Bildmenge keine negativen reellen Zahlen auftreten. Für den Mathematiker gäbe es somit keine Umkehrfunktion, es sei denn, die Bildmenge wird auf die Menge der positiven reellen Zahlen unter Ausschluss der Null eingeschränkt. Der Logarithmus von null ist nicht definiert.
Arkusfunktion
Die Umkehrfunktion einer Winkelfunktion ist deren Arkusfunktion. Winkelfunktionen sind periodisch und weder injektiv noch surjektiv und ihre Umkehrfunktionen können mathematisch nur für einen entsprechend eingegrenzten Definitions- und Wertebereich angegeben werden. Im Folgenden soll die Umkehrfunktion nur für die Sinusfunktion gezeigt werden. Streng monoton verläuft die Sinuskurve nur im Bereich 90° bis 270° oder −90° bis +90°. Die maximale Amplitude für f(x) = sin(x) nimmt Werte zwischen +1 bis −1 an. Für die Variable kann ein Winkelwert oder sein Bogenmaß eingesetzt werden. Das Ergebnis ist eine reelle Zahl. Die Umkehrfunktion f(x) = arcsin(x) = asin(x) gibt für eine reelle Variable entweder das Bogenmaß oder den Winkelwert zurück. Der Taschenrechner muss entsprechend eingestellt sein.
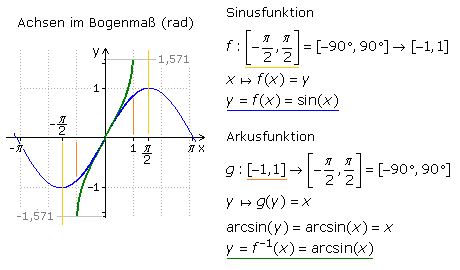
Ist der Taschenrechner auf Gradmaß (DEG) eingestellt, dann wird für sin(90°) = 1 der Maximalwert der Amplitude angezeigt. Die Umkehrfunktion liefert für diesen Wert mit arcsin(1) = 90° den Winkel zurück. Ist das Bogenmaß (RAD) eingestellt, dann folgt für sin(π/2) = sin(1,571) = 1. Die Umkehrfunktion errechnet mit arcsin(1) = 1,571 das Bogenmaß, das dem Winkel 90° entspricht. Auf dem Taschenrechner wird die Umkehrfunktion durch sin−1 angezeigt und ist nicht mit dem mathematischen Kehrwert zu verwechseln.