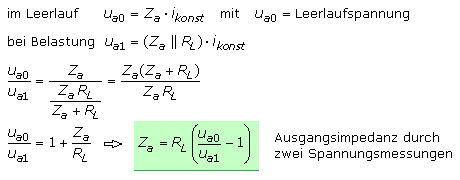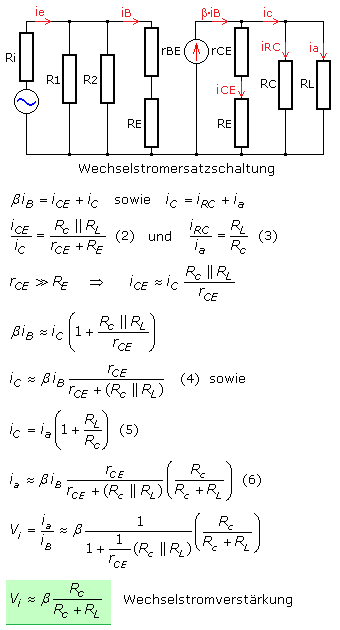Der Kleinleistungsverstärker in Emitterschaltung

Viele universelle Verstärkerschaltungen sind (wurden) mit bipolaren Transistoren in der Emittergrundschaltung aufgebaut. Dieses Kapitel beschreibt einen einstufigen Kleinsignalverstärker ausführlich in mehreren Abschnitten. Jede aktive Baugruppe und somit jede Verstärkerschaltung benötigt eine Gleichstromversorgung. Dem Verstärker muss ein definierter statischer Arbeitspunkt zugewiesen werden. Im Bereich des DC-Arbeitspunktes können dann dynamische Eingangssignale wie zum Beispiel Sprache oder Musik weitgehend unverzerrt verstärkt werden. Der Arbeitspunkt wird nach dem ohmschen Gesetz berechnet und sollte gegen äußere Einflüsse, in erster Linie Temperaturschwankungen, stabilisiert sein. Das Schaltungskonzept sollte aber auch die im Reparaturfall auftretenden unterschiedlichen Eigenschaften der Transistoren, wie Exemplarstreuungen bei gleichen Typen, ausgleichen können. Im Kapitel der Transistorverstärker in Emitterschaltung sind die Grundlagen der Arbeitspunktstabilisierung ausführlich beschrieben worden.

Ein Kleinsignalverstärker entspricht fast immer einem Class-A Verstärker. Zur statischen DC-Berechnung wird davon ausgegangen, dass der Arbeitspunkt des Verstärkers ungefähr auf der Mitte der Arbeitsgeraden liegt. Steuert ein Eingangssignal den Verstärker an, so liegt das verstärkte Ausgangssignal symmetrisch um den Arbeitspunkt. An anderer Stelle in diesem Webprojekt wird die Arbeitsweise eines Transistors im Kennlinienfeld per Videoclip gezeigt und beschrieben, welchen Einfluss die Lage des Arbeitspunktes auf das Ausgangssignal hat.

Die Berechnung des statischen Arbeitspunkts

Nachfolgend wird ein einstufiger Transistorverstärker mit dem BC 548 B in Emitterschaltung berechnet, um anschließend seine Signaleigenschaften zu untersuchen. Die wichtigsten Eigenschaften werden messtechnisch ermittelt und theoretisch erklärt. Vorgesehen ist der Class-A Betrieb, bei dem der DC-Arbeitspunkt auf der halben Betriebsspannung liegt. Dem Datenblatt lassen sich folgende Werte entnehmen:
Ptot = 0,5 W, ICmax = 100 mA, UCE = 30 V, B ≈300, Transitfrequenz = 300 MHz.

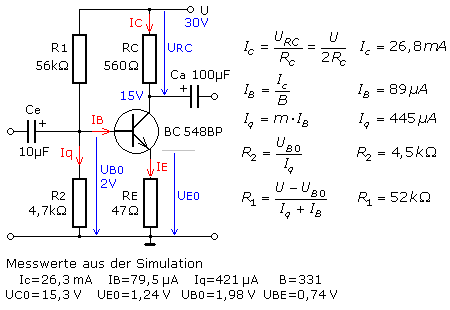
Für die Betriebsspannung sind 30 V Gleichspannung und für den Kollektor- oder Arbeitswiderstand 560 Ω vorgesehen. Ein kleiner Emitterwiderstand von 47 Ω wird die thermische Stabilisierung des Arbeitspunkts sichern. Für ein konstantes Basispotenzial werden 2 V bei einem Querstromfaktor von m = 5 angesetzt. Als Basisstromverstärkung wird B = 300, der Wert des Datenblatts angenommen. Mit diesen Angaben kann die Schaltung skizziert werden, um die fehlenden Bauteile zu berechnen. Abweichend von der Berechnung werden Widerstandswerte einer E-Normreihe eingesetzt. Die aufgebaute Schaltung zeigt, dass die vorgegebenen Werte recht gut erreicht werden, egal ob im Labor mit realen Bauteilen oder im Simulationsprogramm gearbeitet wird.

Die kapazitive Kopplung

Die Schaltung hat am Ein- und Ausgang Kondensatoren zur kapazitiven Kopplung der AC-Signale. Das Verfahren hat den Vorteil, dass sich der berechnete statische DC-Arbeitspunkt des Transistorverstärkers beim Anschließen einer Signalquelle oder einer Ausgangslast nicht ändert. Die Kondensatoren sind für Gleichstrom hochohmig und der Verstärker ist nach außen hin galvanisch entkoppelt. Von Nachteil ist, dass der Verstärker keine Gleichspannungen und Gleichströme verstärken kann und seine Bandbreite eingeschränkt ist. Damit die Verstärkung tiefer Frequenzen nicht zu sehr gedämpft wird, müssen die Kondensatoren ausreichend hohe Kapazitätswerte haben. Werden Elektrolytkondensatoren verwendet, ist beim Einbau auf die richtige Polung zu achten.

Das verstärkte Ausgangssignal ist am Kollektor des Transistors gegen Schaltungsmasse messbar. Beim Class-A Verstärker liegt dieser Messpunkt ungefähr auf der halben DC-Betriebsspannung. Das Ausgangssignal direkt am Kollektor ist die Überlagerung des AC-Signals mit der DC-Arbeitspunktspannung. Diese Mischspannung wird erst nach dem Auskoppelkondensator zum null symmetrischen AC-Signal, da der DC-Anteil durch den in Reihe geschalteten Koppelkondensator geblockt wird.

Die Signaleigenschaften des Emitterverstärkers

Die Signaleigenschaften eines Verstärkers sollten nur mithilfe definierter Testsignale untersucht werden. Bei Audioverstärkern sind Sprach- oder Musiksignale ungeeignet, auch wenn sie später gerade dafür verwendet werden. Niederfrequenz- und Audioverstärker werden mit monofrequenten Sinussignalen getestet. Das wichtigste Testsignal im Audiobereich ist der 1 kHz Sinuston.

Die Sinus-Dauerleistung

In den Betriebsdaten eines Verstärkers gibt der Hersteller für den Ausgang eine minimale Lastimpedanz an. Dieser Widerstandswert sollte nicht unterschritten werden, um dem Gerät keinen Schaden zuzufügen. Der oben berechnete Transistorverstärker gibt an seinem Arbeitswiderstand von 560 Ω seine maximale Leistung ab, wenn der angeschlossene Lastwiderstand ebenso groß ist. Die Leistungsanpassung mit maximaler Leistungsabgabe ist gegeben, wenn die Ausgangsimpedanz (Innenwiderstand) des Verstärkers gleich der angeschlossenen Lastimpedanz ist. Die Messung der Sinusdauerleistung findet bei Vollaussteuerung und Anschluss der vorgeschriebenen Nennimpedanz statt.

Zur Messung wird an den Eingang der Schaltung das Audiotestsignal 1 kHz Sinus gelegt. Der Ausgang wird mit der Nennimpedanz belastet. Die Amplitude des Eingangssignals wird solange erhöht, wie das Ausgangssignal noch unverzerrt sinusförmig messbar ist. Ein Audioverstärker muss diese Leistung nach der DIN Hi-Fi Messvorschrift für mindestens 10 Minuten bei einem definierten Klirrfaktor von maximal 0,7% erbringen.

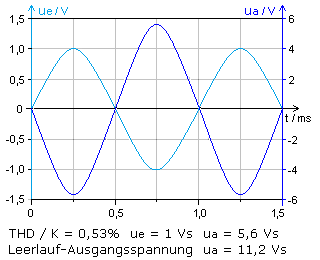
Nach dieser Messvorschrift wurde der Emitterverstärker im Simulationsprogramm untersucht. Die Nennimpedanz betrug 560 Ω. Der Gesamtklirrfaktor bei Leistungsanpassung betrug 0,53% für die Referenzfrequenz von 1 kHz. Für Leistungsanpassung beträgt die effektive Sinusdauerleistung des Verstärkers:
P = (0,707·5,6 V)² / 560 Ω = 28 mW.
Die Ausgangsspannung des unbelasteten Verstärkers ist doppelt so hoch. Damit kann die Leerlaufverstärkung berechnet werden:
Vu = ua/ue = 11,2 V / 1 V = 11,2 oder 21 dB.
Die Wechselstrommessungen ergaben für den Basisstrom iB = 58,5 μA und den Kollektorstrom iC = 14,3 mA. Die daraus folgende Wechselstromverstärkung beträgt β = 244.

Das Übertragungsverhalten – Frequenzgang des Verstärkers

Kein Verstärker wird alle Frequenzen gleich gut verstärken. Durch eine AC-Frequenzanalyse, dem Amplitudenfrequenzgang als Teil des Bodediagramms, erhält man eine Aussage über die Linearität des Verstärkers, die obere und untere Grenzfrequenz und damit die Übertragungsbandbreite. Im Bodediagramm wird auch der Phasenverlauf im Frequenzbereich aufgezeichnet. Sind keine speziellen Messvorschriften erforderlich, so gilt für die Messung des Frequenzgangs an Niederfrequenz- und Audioverstärker die folgende Grundeinstellung:

Die Vollaussteuerung wird für die Normfrequenz von 1 kHz Sinussignal vorgenommen. Die Messungen erfolgen bei einem Eingangssignalpegel von 20 dB unter Vollaussteuerung.
Bei Hi-Fi Kombinationsanlagen werden nach DIN 45500 bei 10 dB unter Nennausgangsleistung im Frequenzbereich von 40 ... 16000 Hz gemessen.

Der Bodeplotter eines Simulationsprogramms ist eine Art Wobbelgenerator für die AC-Frequenzanalyse einer Schaltung. Das Programm berechnet das Messergebnis für die Signalvollaussteuerung und weicht damit von der üblichen Messmethode ab. Der Verlauf des Phasendiagramms sollte nicht ungeprüft übernommen werden. Das folgende Bild zeigt die Simulationsergebnisse für den Frequenzgang und Phasengang der Emitterschaltung.

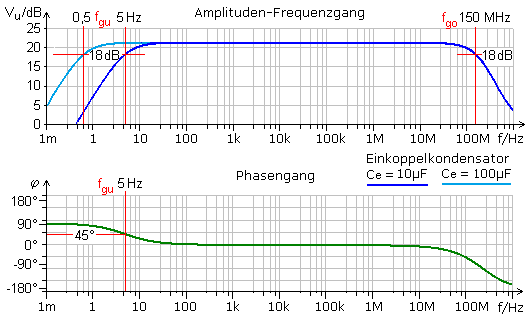
Die Verstärkerschaltung hat einen linearen Frequenzgang sehr großer Bandbreite. Man könnte nachweisen, dass die obere Grenzfrequenz vom Ein- und Auskoppelkondensator unabhängig ist. Die untere Grenzfrequenz wird durch den Eingangskondensator beeinflusst. Er bildet mit dem Eingangswiderstand der Schaltung einen Hochpass. Kleinere Kapazitätswerte ergeben eine höhere untere Grenzfrequenz. Je höher der Eingangswiderstand ist, desto kleiner kann der Koppelkondensator bei gleicher Grenzfrequenz sein.

Bei der unteren Grenzfrequenz ist der Phasenwinkel wie erwartet mit φ = +45° ablesbar. Errechnet man für die untere Grenzfrequenz den Blindwiderstand des Einkoppelkondensators, so lässt sich daraus der Eingangswiderstand der Transistorschaltung mit rund 3,2 kΩ ermitteln. Die Messung des Eingangswiderstands erfolgt zu einem späteren Zeitpunkt. Nach dem Phasendiagramm liegt die obere Grenzfrequenz bei 80 MHz, dort zeigt sich Tiefpassverhalten mit φ = −45°. Die Übertragungsbandbreite des Verstärkers reicht bis 150 MHz.

Die Wechselstromersatzschaltung des Transistorverstärkers

Jede Gleichspannungsversorgung ist vergleichbar mit einem aufgeladenen Kondensator sehr großer Kapazität. Der Blindwiderstand eines 10000 μF-Kondensators, ein für gute traditionelle Netzteile üblicher Wert, beträgt für die Signalfrequenz von 10 Hz nur 1,59 Ω und ist somit vernachlässigbar klein. Beide Pole der DC-Betriebsspannung besitzen für ein periodisches Wechselsignal das gleiche Potenzial, folglich kann parallel dazu keine Signalspannung gemessen werden. Die Transistorschaltung kann in ein Wechselstrom Ersatzschaltbild umgezeichnet werden. Der Ein- und Auskoppelkondensator ist kein notwendiger Bestandteil der Schaltung. Im Signalersatzschaltbild wird er weggelassen oder als Wechselstromkurzschluss angesehen. In einer AC-Ersatzschaltung treten nie Gleichspannungen oder Gleichströme auf.

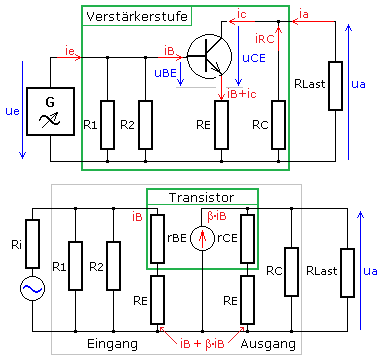
Alle AC-Signalgrößen sollten mit kleinen Buchstaben bezeichnet werden. Am Transistoreingang befindet sich zwischen Basis und Emitter der dynamische Eingangswiderstand rBE. Am Transistorausgang liegt zwischen Kollektor und Emitter der dynamische Ausgangswiderstand rCE. Der Basisstrom wird mit dem Stromverstärkungsfaktor β verstärkt. Die Ausgangsseite wird als Ersatzstromquelle mit β·iB definiert.

Ein Emitterwiderstand wirkt sich sowohl auf den Eingang als auch auf den Ausgang in unterschiedlichem Maß aus. Dieser Widerstand wird vom Basisstrom und vom Kollektorstrom durchflossen. Auf der Ausgangsseite ist iB « iC, somit ist der Anteil des Basisstroms vernachlässigbar. Die Widerstände rCE und RE bilden eine Reihenschaltung, wobei RE « rCE ist und meistens nicht berücksichtigt werden muss.

Auf den Eingang der Verstärkerstufe wirkt der Emitterwiderstand mit dem um den Stromverstärkungsfaktor β multiplizierten Wert. Der Basisstrom ist zum Kollektorstrom gleichphasig und addiert sich zum Emitterstrom. Für die Steuerspannung am Transistor bleibt nur ein kleiner Teil von ue wirksam. Die AC-Eingangsspannung teilt sich an der Reihenschaltung aus rBE und (1 + β)·RE auf.

Die Eingangsimpedanz der Verstärkerstufe

Am Eingang des Wechselstromersatzschaltbilds bilden die beiden Widerstände des Basisspannungsteilers eine Parallelschaltung. Sie liegen auch parallel zur Reihenschaltung aus dem dynamischen Basis-Emitter-Bahnwiderstand des Transistors und dem angepassten Emitterwiderstand β·RE.

Der Stufeneingangswiderstand kann insgesamt nur mittelhoch sein. Im Basisspannungsteiler sollte der Wert des Fußpunktwiderstands möglichst hochohmig sein, da sein Einfluss in der Parallelschaltung groß ist. Ohne Emitterwiderstand bestimmt der niedrige dynamische Transistor Eingangswiderstand rBE den Eingangswiderstand der Stufe. Eine Verkleinerung des Basisstroms erhöht den Wert von rBE, mindert aber die Spannungsverstärkung, da bei kleinerem iB auch die Steuerspannung uBE geringer ist.

Der Koppelkondensator bildet mit dem Eingangswiderstand eine Hochpassschaltung und bestimmt die untere Grenzfrequenz. Aus dem Messwert für fgu wurde weiter oben der Widerstandswert zu 3,2 kΩ errechnet. Dieser Wert ist identisch mit dem aus der hergeleiteten Gleichung Gl.(1).

Messung nach der Methode der halben Ausgangsspannung:

Der Eingangswiderstand (Eingangsimpedanz) der Verstärkerstufe ist messtechnisch einfach zu ermitteln. An den Eingang wird das 1 kHz sinusförmige Testsignal angelegt und die Amplitude so weit vergrößert, dass die Ausgangsspannung maximal wird, aber unverzerrt bleibt. Das konstant gehaltene Eingangssignal wird dann über einen verstellbaren Widerstand an den Verstärker gelegt. Der Widerstandswert wird solange vergrößert, bis die Amplitude am Ausgang nur noch den halben Wert der ersten Messung hat. Unter der Voraussetzung einer linearen Verstärkung liegt am Verstärkereingang dann ebenfalls die halbe Signalamplitude an. Das konstante Quellensignal hat sich je zur Hälfte auf die Spannung am Stellwiderstand und am Verstärkereingang aufgeteilt. Da Spannungen und Widerstandswerte einander proportional sind, entspricht der Wert des Stellwiderstands dem zu bestimmenden Eingangswiderstand (Eingangsimpedanz) des Verstärkers. Die Skizze veranschaulicht die allgemeine Messmethode zur Bestimmung der Eingangsimpedanz einer Schaltung.

Die Ausgangsimpedanz der Verstärkerstufe

Die Kennlinien eines Transistors verlaufen im Ausgangskennlinienfeld bei konstantem Basissteuerstrom fast parallel zur Abszisse, der UCE-Achse. Aus der Steigung der Kennlinie im Arbeitsbereich kann für jeden Basisstromparameter ein Ausgangsleitwert errechnet werden. Sein Kehrwert ist der dynamische Ausgangswiderstand des Transistors rCE, der einige Kiloohm beträgt.

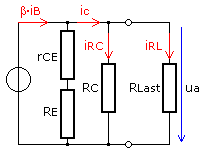
In der Signalersatzschaltung ist der Transistor auf der Ausgangsseite als Stromquelle definiert, die den Strom β·iB liefert. Er teilt sich in die Zweigströme der parallel liegenden Widerstände rCE, dem Arbeitswiderstand RC und einem angeschlossenen Lastwiderstand RL auf. Der dynamische Transistorwiderstand rCE und RE bilden eine Reihenschaltung. In ihr bestimmt der hochohmige rCE den Wert und der viel kleinere RE ist vernachlässigbar. Die unbelastete Ausgangsimpedanz wird meistens nur vom kleineren Kollektor-(Arbeits)-Widerstand bestimmt.

Messung nach der Methode der halben Ausgangsspannung

Der Transistor erzeugt als Ersatzstromquelle mit iC am Kollektor-(Arbeits)-Widerstand die Leerlaufausgangsspannung. Wird sie durch einen parallel geschalteten einstellbaren Lastwiderstand belastet, so teilt sich der Strom in die beiden Teilströme iRC und iRL auf. Sind beide Ströme gleich groß, dann sind auch die Widerstände gleich groß. Durch RC und RL fließt der halbe Kollektorstrom. Durch diese Belastung ist die Leerlaufspannung am Ausgang auf die Hälfte zurückgegangen. Wird der Ausgangswiderstand dieser Schaltung im Simulationsprogramm nach der Methode der halben Ausgangsspannung ermittelt, so ist das Ergebnis Zaus = 560 Ω, und entspricht dem theoretisch hergeleiteten Ergebnis.

Bei Leistungsverstärkern darf die Ausgangsimpedanz nicht nach der Methode der halben Ausgangsspannung bestimmt werden.

Messung nach der ΔU-, ΔI-Methode

Um eine niederohmige Verstärkerendstufe bei der messtechnischen Bestimmung ihrer Ausgangsimpedanz nicht zu überlasten, soll die vom Hersteller angegebene Anschlussimpedanz, oftmals 4 Ω, nicht unterschritten werden. Die interne Quellenimpedanz kann wenige 100 Milliohm betragen. Die Ausgangsimpedanz lässt sich durch zwei Spannungsmessungen errechnen. Man bestimmt die Leerlaufspannung und anschließend die Ausgangsspannung an einem Lastwiderstand im erlaubten Rahmen. Die Bestimmungsgleichung für Za zeigt die folgende Herleitung.

Ist die Bestimmungsgleichung und ihre Herleitung unbekannt, wird zuerst die Leerlaufspannung gemessen. Danach wird der Ausgang mit einem bekannten Widerstand belastet und die nun kleinere Ausgangsspannung gemessen. Mithilfe des ohmschen Gesetzes kann jetzt der Ausgangsstrom durch den Lastwiderstand berechnet werden. Die zu bestimmende Ausgangsimpedanz der Schaltung ist ihr Innenwiderstand, der mit dem Lastwiderstand eine Reihenschaltung bildet. Aus der Spannungsdifferenz bei dem errechneten Strom kann mit dem ohmschen Gesetz die Ausgangsimpedanz der Schaltung errechnet werden. Die folgende Messwerttabelle bestätigt für zwei unterschiedliche Belastungen die Richtigkeit der Aussagen. Die Leerlaufspannung betrug u0 = 8,024 V.

Die Wechselstromverstärkung

Für die folgenden Betrachtungen hat die Schaltung einen zuvor berechneten DC-Arbeitspunkt. Die Ausführungen betreffen die AC-Signalgrößen. Die Eingangswechselspannung erzeugt an der Steuerstrecke des Transistors den AC-Basisstrom. Sofern kein Emitterwiderstand vorhanden ist, sind die Verhältnisse übersichtlich und mathematisch einfach zu lösen. Mit einem Emitterwiderstand muss der dynamische Verstärkungsfaktor β bekannt sein, da am Eingang das Produkt β·RE der wirksamere Widerstand ist. Er bestimmt mit dem in Reihe liegenden viel kleineren rBE weitgehend den Basisstrom.

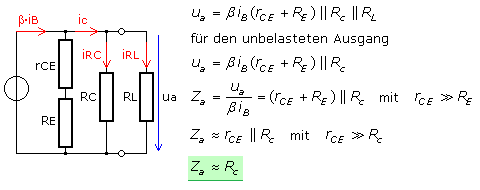
Der Transistor erzeugt als Stromquelle den Ausgangswechselstrom β·iB. Dieser Strom teilt sich in die Zweigströme durch rCE, RC und RLast auf. Mithilfe der Signalersatzschaltung werden für den Ausgang die Beziehungen der Teilströme aufgestellt. Sie verhalten sich umgekehrt proportional zu den Widerständen Gl.(2) und Gl.(3).

Man kann in guter Näherung davon ausgehen, dass der dynamische Transistorinnenwiderstand rCE sehr groß gegen den Emitterwiderstand RE ist. Mit der vereinfachten Gl.(2) ergibt sich mit Gl.(3) nach dem Einsetzen in die anfänglichen Stromgleichungen eine Beziehung Gl.(4) für den Kollektorstrom. Für ihn kann ebenso die Gleichung Gl.(5) aufgestellt werden.

Durch Gleichsetzen von Gl.(4) und Gl.(5) erhält man mit Gl.(6) eine Formel für den Ausgangsstrom ia. Die Stromverstärkung errechnet sich aus dem Verhältnis der Ströme β·iB zu iB.

Da rCE im Vergleich zur Parallelschaltung sehr groß ist, kann für den ersten Bruch in guter Näherung der Wert 1 gesetzt werden. Für die Stromverstärkung erhält man eine übersichtliche Formel.

Ein Transistor in Emitterschaltung hat eine hohe Stromverstärkung.
Sie verringert sich bei Belastung mit RLast oder der Eingangsimpedanz einer Folgestufe.

Die Wechselspannungsverstärkung

Ausschlaggebend für die folgenden Betrachtungen sind die AC-Werte für eine Schaltung mit zuvor berechnetem DC-Arbeitspunkt. Der Emitterwiderstand wird sowohl vom Basisstrom als auch vom Kollektorstrom, dem mit β verstärkten Basisstrom durchflossen. Die Eingangsspannung ue teilt sich an der Reihenschaltung rBE und β·RE auf. Nur die am dynamischen Transistorwiderstand rBE verbleibende Teilspannung erzeugt letztlich den Basisstrom iB. Der Transistor liefert mit β·iB am Kollektorwiderstand die Leerlaufausgangsspannung ua. Mit der Berücksichtigung aller Widerstände ist die Spannungsverstärkung das Verhältnis von ua zu ue.

Ein Transistor in Emitterschaltung hat eine hohe Spannungsverstärkung.
Mit einem Emitterwiderstand ist die Spannungsverstärkung infolge der Stromgegenkopplung geringer.
Die Belastung mit RL oder der Eingangsimpedanz einer Folgestufe verkleinert die Verstärkung.

Bandbreite des Verstärkers

Die Stromgegenkopplung und die Grenzfrequenzen

Der hier untersuchte Transistorverstärker hat einen Emitterwiderstand zur Stromgegenkopplung und Arbeitspunktstabilisierung. Mit ihm wird die Schaltung auch unempfindlich gegen Exemplarstreuungen beim Ersatz des Transistors. Sehr wichtig ist der Einfluss von RE zur Linearisierung der Verstärkung und Verringerung der Verzerrungen im Ausgangssignal. Neben allen Vorteilen kommt es zur Herabsetzung der maximal möglichen Spannungsverstärkung.

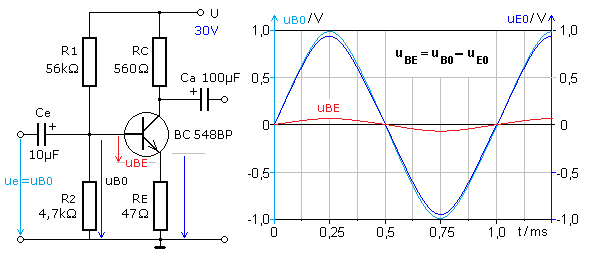
Der verstärkte Basisstrom fließt als Emitterstrom durch den Emitterwiderstand und verursacht die Emitterspannung. Sie ist zur Eingangsspannung gleichphasig. Der Transistor verstärkt nur die Spannungsdifferenz uBE an der Basis-Emitterstrecke. Das anliegende AC-Eingangssignal ist für die Basisspannung uB0 verantwortlich. Wird die AC-Spannung am Emitterwiderstand uE0 davon subtrahiert, folgt daraus die wirksame aber kleinere Steuerspannung uBE. Mit einem kleineren Emitterwiderstand wird die gleiche Verstärkung mit einer kleineren Eingangsspannung erreicht. Die Grafik zeigt die bei Stromgegenkopplung auftretenden Spannungen, die zur Steuerspannung (rot) am Transistor führen.

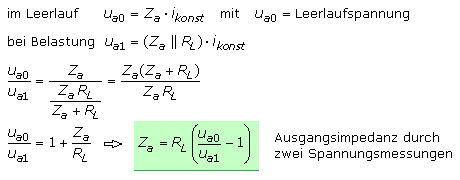
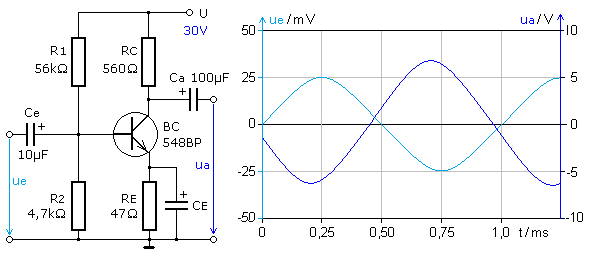
Eine größere Signalverstärkung oder die gleiche Verstärkung bei kleinerem Eingangssignal kann durch das Parallelschalten eines Kondensators zu RE erreicht werden. Kondensatoren sind frequenzabhängige Widerstände, die zu höheren Frequenzen niederohmig werden. Bei entsprechender Dimensionierung ist der zum Emitterwiderstand parallel geschaltete Kondensator so niederohmig, dass er die Signalgegenkopplung praktisch aufhebt. Da der Kondensator für Gleichstrom einen extrem hohen Widerstand besitzt, hat er keinen negativen Einfluss auf die Stabilisierung des DC-Arbeitspunkts.

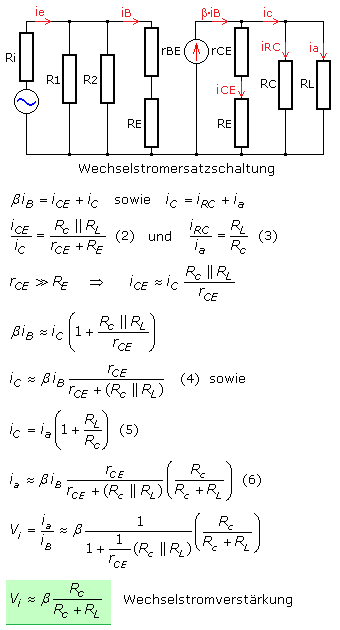
Ohne Emitterkondensator hatte der Transistor eine Leerlaufverstärkung von Vu = 11. Mit CE = 220 ... 470 μF nimmt die Verstärkung bei unverzerrtem Ausgangssignal auf Vu = 260 zu. Die maximale Spitzenspannung von 11 V am Ausgang beim nicht verzerrten Sinussignal mit wirksamem RE wird bei aufgehobener Signalgegenkopplung durch CE nicht mehr erreicht. Die dargestellten 6,5 Vs sind das Maximum. Die Stromverstärkung bleibt unbeeinflusst. Die Leistungsverstärkung als das Produkt aus Strom- und Spannungsverstärkung erreicht mit CE ebenfalls viel höhere Werte.

Die untere Grenzfrequenz der Emitterschaltung

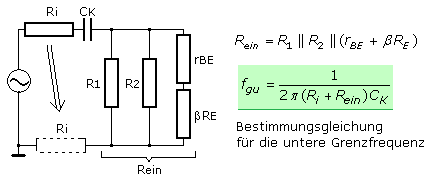
Am Anfang der Seite wurde das Übertragungsverhalten des Verstärkers mit aktiver Stromgegenkopplung dargestellt. Verantwortlich für die untere Grenzfrequenz ist der Einkoppelkondensator in Verbindung mit der Eingangsimpedanz der Schaltung. Zusammen bilden beide einen Hochpass. Manchmal muss auch noch der Generatorinnenwiderstand, die Ausgangsimpedanz einer Vorstufe, mit berücksichtigt werden, da auch er zur Eingangsimpedanz in Reihe liegt. Die weiter oben berechnete und messtechnisch ermittelte Eingangsimpedanz betrug 3,2 kΩ. Der Einkoppelkondensator hat eine Kapazität von 10 μF. Die untere Grenzfrequenz des gegengekoppelten Transistorverstärkers errechnet sich zu 5 Hz und entspricht dem Messwert im Bodediagramm.

Wird die Signalgegenkopplung durch einen Emitterkondensator aufgehoben, so liegt das Eingangssignal an der Reihenschaltung von rBE und CE. Das entspricht auch einem Hochpass, denn das den Transistor ansteuernde Signal liegt nur am dynamischen Widerstand rBE. Der zur Hochpassschaltung parallele Basisspannungsteiler hat keinen Einfluss auf die Grenzfrequenz. Der Basis- und der Kollektorstrom beeinflussen den Emitterkreis, folglich wirken der Emitterkondensator und der Verstärkungsfaktor β mit großem Einfluss auf die untere Grenzfrequenz. Die Herleitung nutzt die Tatsache, dass bei jeder Grenzfrequenz der Realanteil gleich dem Blindanteil ist.

Werden beide Bestimmungsgleichungen für fgu miteinander verglichen, so ist zu erkennen, dass sich der Emitterkondensator weitaus negativer als der Einkoppelkondensator auf die untere Grenzfrequenz auswirkt und sie in den Bereich höherer Frequenzen schiebt. Sind in der Schaltung sowohl ein Koppelkondensator und der Emitterkondensator vorhanden, dann bilden beide eine Reihenschaltung. In der folgenden Bestimmungsgleichung sind beide Kondensatoren berücksichtigt.

Zur Berechnung muss die Eingangsimpedanz der Stufe für die Wechselspannung bekannt sein. Sie ist ohne wirksamen Emitterwiderstand wesentlich niedriger und wird dabei nur durch den dynamischen Eingangswiderstand des Transistors rBE bestimmt. Für die untersuchte Schaltung wurde er anfangs aus einer Strom-, Spannungsmessung zu 535 Ω errechnet. Bei der experimentellen Bestimmung nach der halben Spannungsmethode liefert das Simulationsprogramm für verschiedene Emitterkondensatoren einen durchschnittlichen Wert von rBE = 480 Ω. Die AC-Frequenzanalyse als Teil des Bodediagramms zeigt die Ergebnisse.

Berechnung der Kapazitätswerte

Bisher wurden die Kapazitätswerte frei gewählt und ihr Einfluss untersucht. In der Praxis sollen zu geforderten Eigenschaften der Verstärker die Bauteile berechnet werden. Zu einer gegebenen unteren Grenzfrequenz sind die Kapazitätswerte der Hochpassglieder zu errechnen.

Bei der Grenzfrequenz ist die Verstärkung um 3 dB geringer. Sind mehrere Hochpassglieder in der Schaltung, so schwächt jede Stufe Das Signal für sich um 3 dB. Bei zwei Pässen sind das 6 dB bei drei 9 dB. Alle Hochpässe zusammen sollen bei der gewünschten unteren Grenzfrequenz des Verstärkers nur mit der Dämpfung 3 dB wirken. Die Einzelstufe muss somit für eine geringere Schwächung berechnet werden.

Mit der Anzahl n der beteiligten Hochpässe wird der Schwächungsfaktor S errechnet. Die zweite Bestimmungsgleichung liefert einen Pseudowert der Grenzfrequenz, der kleiner ist als die gewünschte Grenzfrequenz fgu. Mit dem Pseudowert können dann die einzelnen Kondensatoren mit den zuvor hergeleiteten Gleichungen errechnet werden. Dabei ist es zu beachten, dass der richtige Eingangswiderstand verwendet wird.

Die obere Grenzfrequenz der Emitterschaltung

Die obere Grenzfrequenz wird von allen Schaltkapazitäten bestimmt, die den Signalweg nach Masse ableiten und daher Tiefpasswirkung zeigen. Der Transistor besitzt in seinen Diodenstrecken sogenannte Sperrschichtkapazitäten. Im NF-Bereich können sowohl die der Kollektor-Emitterstrecke CCE und der Basis-Emitterstrecke CBE vernachlässigt werden, da sie nur wenige Picofarad betragen.

Auf die Ausgangsspannung ua bezogen bildet die Kollektor-Basiskapazität CCB mit dem Eingangswiderstand re einen Hochpass. Die Spannung teilt sich auf in uC und ue. Zu höheren Frequenzen wird die Spannung am Kondensator kleiner und an re entsprechend größer. Da die Emitterschaltung ein zum Eingang gegenphasiges Signal liefert, wird mit zunehmender Frequenz das eigentliche Eingangssignal immer mehr gedämpft. Es handelt sich um eine frequenzabhängige Rückkopplung in Form der Spannungsgegenkopplung.

Ein einem eigenen Kapitel werden spezielle Informationen zur Rückkopplung gegeben. Hier werden nur die Verhältnisse für die obere Grenzfrequenz hergeleitet, wo die aktuelle Verstärkung bei Gegenkopplung V um 3 dB geringer ist als Vo ohne Gegenkopplung. Der Koppelfaktor k nach Gl.(9) entspricht dem Spannungsverhältnis ue zu ua, das proportional zu entsprechenden Widerständen ist.

Die mit dieser Bestimmungsgleichung berechnete obere Grenzfrequenz konnte messtechnisch an einer realen Transistorschaltung bestätigt werden. In den Datenblättern wird für die Kollektor-Basiskapazität ein typischer Wert von 2 pF angegeben. Mit der zuletzt gemessenen Spannungsverstärkung von Vu = 260 und dem Eingangswiderstand re = 480 Ω errechnet sich die Grenzfrequenz zu fgo = 265 kHz.

Für die Transitfrequenz des BC 548 werden 300 MHz angegeben. Mithilfe des konstanten Bandbreite-Verstärkungsprodukts würde bei der Verstärkung V = 260 für fgo 1 MHz zu erwarten sein. Die Simulationssoftware lieferte in diesem Fall kein sinnvolles Ergebnis.

Zusammenfassung der Eigenschaften der Emitterschaltung

Die Emitterschaltung ist universell anwendbar. Meistens wird sie mit Stromgegenkopplung und Basisspannungsteiler betrieben. Sie zeichnet sich durch eine hohe Spannungs- und Stromverstärkung aus und hat daher eine hohe Leistungsverstärkung. Es ist die einzige Transistorschaltung mit einer Inversion oder Phasendrehung von 180° zwischen Eingangs- und Ausgangssignal. Mit einer AC-Stromgegenkopplung bleiben selbst bei hoher Verstärkung die nichtlinearen Verzerrungen im Ausgangssignal gering. Zu den Nachteilen kann die teilweise niedrige bis mittelhohe Eingangsimpedanz zählen. Für hohe Frequenzen ist bei großer Verstärkung die Rückwirkkapazität der Kollektor-Basis-Sperrschicht störend. Durch sie wird die Verstärkung frequenzabhängig.